Buffers

> >

In the previous chapter, a production system was discussed that passes values from one process to the next using channels, in a synchronous manner. (Sender and receiver perform the communication at exactly the same moment in time, and the communication is instantaneous.) In many systems however, processes do not use synchronous communication, they use asynchronous communication instead. Values (products, packets, messages, simple tokens, and so on) are sent, temporarily stored in a buffer, and then received.

In fact, the decoupling of sending and receiving is very important, it allows compensating temporarily differences between the number of items that are sent and received. (Under the assumption that the receiver is fast enough to keep up with the sender in general, otherwise the buffer will grow forever or overflow.)

For example, consider the exchange of items from a producer process P to a consumer process C as shown in the following figure:

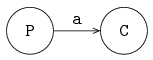
In the unbuffered situation, both processes communicate at the same time. This means that when one process is (temporarily) faster than the other, it has to wait for the other process before communication can take place. With a buffer in-between, the producer can give its item to the buffer, and continue with its work. Likewise, the consumer can pick up a new item from the buffer at any later time (if the buffer has items).

In Chi, buffers are not modeled as channels, they are modeled as additional processes instead. The result is shown in the following figure:

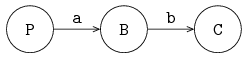
The producer sends its items synchronously (using channel a) to the buffer process. The buffer process keeps the item until it is needed. The consumer gets an item synchronously (using channel b) from the buffer when it needs a new item (and one is available).

In manufacturing networks, buffers, in combination with servers, play a prominent role, for buffering items in the network. Various buffer types exist in these networks: buffers can have a finite or infinite capacity, they have a input/output discipline, for example a first-out queuing discipline or a priority-based discipline. Buffers can store different kinds of items, for example, product-items, information-items, or a combination of both. Buffers may also have sorting facilities, etc.

In this chapter some buffer types are described, and with the presented concepts numerous types of buffer can be designed by the engineer. First a simple buffer process with one buffer position is presented, followed by more advanced buffer models. The producer and consumer processes are not discussed in this chapter.

A one-place buffer

A buffer usually has a receiving channel and a sending channel, for receiving and sending items. A buffer, buffer B1, is presented in the figure below:

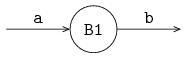
The simplest buffer is a one-place buffer, for buffering precisely one item. A one-place buffer can be defined by:

proc B1(chan? item a; chan! item b):
    item x;

    while true:
        a?x; b!x
    end
end

where a and b are the receiving and sending channels. Item x is buffered in the process. A buffer receives an item, stores the item, and sends the item to the next process, if the next process is willing to receive the item. The buffer is not willing to receive a second item, as long as the first item is still in the buffer.

A two-place buffer can be created, by using the one-place buffer process twice. A two-place buffer is depicted below:

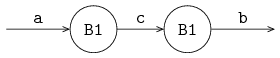
A two-place buffer is defined by:

proc B2(chan? item a; chan! item b):
    chan item c;

    run B1(a, c), B1(c, b)
end

where two processes B1 buffer maximal two items. If each process B1 contains an item, a third item has to wait in front of process B2. This procedure can be extended to create even larger buffers. Another, more preferable manner however, is to describe a buffer in a single process by using a select statement and a list for storage of the items. Such a buffer is discussed in the next section.

A single process buffer

An informal description of the process of a buffer, with an arbitrary number of stored items, is the following:

If the buffer has space for an item, and can receive an item from another process via channel a, the buffer process receives that item, and stores the item in the buffer.
If the buffer contains at least one item, and the buffer can send that item to another process via channel b, the buffer process sends that item, and removes that item from the buffer.
If the buffer can both send and receive a value, the buffer process selects one of the two possibilities (in a non-deterministic manner).
If the buffer cannot receive an item, and cannot send an item, the buffer process waits.

Next to the sending and receiving of items (to and from the buffer process) is the question of how to order the stored items. A common form is the first-in first-out (fifo) queuing discipline. Items that enter the buffer first (first-in) also leave first (first-out), the order of items is preserved by the buffer process.

In the model of the buffer, an (ordered) list of type item is used for storing the received items. New item x is added at the rear of list xs by the statement:

xs = xs + [x]

The first item of the list is sent, and then deleted with:

xs = xs[1:]

An alternative solution is to swap the function of the rear and the front, which can be useful some times.

The statement to monitor several channels at the same time is the select statement. The syntax of the select statement, with two alternatives, is:

select
    boolean_expression_1, communication statement_1:
        statement_list_1
alt
    boolean_expression_2, communication statement_2:
        statement_list_2
...
end

There has to be at least one alternative in a select statement. The statement waits, until for one of the alternatives the boolean_expression holds and communication using the communication statement is possible. (When there are several such alternatives, one of them is non-deterministically chosen.) For the selected alternative, the communication statement is executed, followed by the statements in the statement_list of the alternative.

The above syntax is the most generic form, the boolean_expression may be omitted when it always holds, or the communication statement may be omitted when there is no need to communicate. The , also disappears then. (Omitting both the boolean expression and the communication statement is not allowed.) Similarly, when the statement_list is empty or just pass, it may be omitted (together with the : in front of it).

The description (in words) of the core of the buffer, from the start of this section, is translated in code, by using a select statement:

select
    size(xs) < N, a?x:
        xs = xs + [x]
alt
    size(xs) > 0, b!xs[0]:
        xs = xs[1:]
end

In the first alternative, it is stated that, if the buffer is not full, and the buffer can receive an item, an item is received, and that item is added to the rear of the list. In the second alternative, it is stated that, if the buffer contains at least one item, and the buffer can send an item, the first item in the list is sent, and the list is updated. Please keep in mind that both the condition must hold and the communication must be possible at the same moment.

The complete description of the buffer is:

proc B(chan? item a; chan! item b):
    list item xs; item x;

    while true:
        select
            size(xs) < N, a?x:
                xs = xs + [x]
        alt
            size(xs) > 0, b!xs[0]:
                xs = xs[1:]
        end
    end
end

Instead of boolean expression size(xs) > 0, expression not empty(xs) can be used, where empty is a function yielding true if the list is empty, otherwise false. In case the capacity of the buffer is infinite, expression size(xs) < N can be replaced by true, or even omitted (including the comma).

An infinite buffer

A buffer with infinite capacity can be written as:

proc B(chan? item a; chan! item b):
    list item xs; item x;

    while true:
        select
            a?x:
                xs = xs + [x]
        alt
            not empty(xs), b!xs[0]:
                xs = xs[1:]
        end
    end
end

A first-in first-out buffer is also called a queue, while a first-in last-out buffer (lifo buffer), is called a stack. A description of a lifo buffer is:

proc B(chan? item a; chan! item b):
    list item xs; item x;

    while true:
        select
            a?x:
                xs = [x] + xs
        alt
            not empty(xs), b!xs[0]:
                xs = xs[1:]
        end
    end
end

The buffer puts the last received item at the head of the list, and gets the first item from the list. An alternative is to put the last item at the rear of the list, and to get the last item from the list.

A token buffer

In the next example, signals are buffered instead of items. The buffer receives and sends 'empty' items or tokens. Counter variable w of type int denotes the difference between the number of tokens received and the number of tokens sent. If the buffer receives a token, counter w is incremented; if the buffer sends a token, counter w is decremented. If the number of tokens sent is less than the number of tokens received, there are tokens in the buffer, and w > 0. A receiving channel variable a of type void is defined for receiving tokens. A sending channel variable b of type void is defined for sending tokens. The buffer becomes:

proc B(chan? void a; chan! void b):
    int w;

    while true:
        select
            a?:
                w = w + 1
        alt
            w > 0, b!:
                w = w - 1
        end
    end
end

Note that variables of type void do not exist. Type void only can be used in combination with channels.

A priority buffer

A buffer for items with different priority is described in this section. An item has a high priority or a normal priority. Items with a high priority should leave the buffer first.

An item is a tuple with a field prio, denoting the priority, 0 for high priority, and 1 for normal priority:

type item = tuple(...; int prio);

For the storage of items, two lists are used: a list for high priority items and a list for normal priority items. The two lists are described by a list with size two:

list(2) list item xs;

Variable xs[0] contains the high priority items, xs[1] the normal priority items. The first item in the high priority list is denoted by xs[0][0], etc.

In the model the received items are, on the basis of the value of the prio-field in the item, stored in one of the two lists: one list for 'high' items and one list for 'normal' items. The discipline of the buffer is that items with a high priority leave the buffer first. The model is:

proc BPrio(chan? item a; chan! item b):
    list(2) list item xs; item x;

    while true:
        select
            a?x:
                xs[x.prio] = xs[x.prio] + [x]
        alt
            not empty(xs[0]), b!xs[0][0]:
                xs[0] = xs[0][1:]
        alt
            empty(xs[0]) and not empty(xs[1]), b!xs[1][0]:
                xs[1] = xs[1][1:]
        end
    end
end

The buffer has two lists xs[0] and xs[1]. Received items x are stored in xs[x.prio] by the statement xs[x.prio] = xs[x.prio] + [x].

If the list high priority items (xs[0]) is not empty, items with high priority are sent. The first element in list xs[0] is element xs[0][0]. If there are no high priority items (list xs[0] is empty), and there are normal priority items (list xs[1] is not empty), the first element of list xs[1], element xs[1][0], is sent.

Note that the order of the alternatives in the select statement does not matter, every alternative is treated in the same way.

Exercises

To study product flow to and from a factory, a setup as shown in the figure below is created:

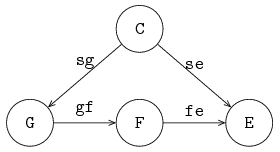
F is the factory being studied, generator G sends products into the factory, and exit process E retrieves finished products. The factory is tightly controlled by controller C that sends a signal to G or E before a product may be moved. The model is as follows:
```
proc G(chan! int a; chan? void sg):
    for i in range(10):
        sg?;
        a!i;
    end
end

proc F(chan? int a; chan! int b):
    ...
end

proc E(chan? int a; chan? void se):
    int x;

    while true:
        se?;
        a?x;
        write("E received %d\n", x);
    end
end

proc C(chan! void sg, se; int low, high):
    int count;

    while true:
        while count < high:
            sg!;
            count = count + 1;
        end
        while count > low:
            se!;
            count = count - 1;
        end
    end
end

model M():
    chan void sg, se;
    chan int gf, fe;

    run C(sg, se, 0, 1),
        G(gf, sg), F(gf, fe), E(fe, se);
end
```
The number of products inserted by the generator has been limited to allow for manual inspection of results.
1. As a model of the factory, use a FIFO buffer process. Run the simulation, and check whether all products are received by the exit process.
2. Change the control policy to low = 1 and high = 4. Predict the outcome, and verify with simulation.
3. The employees of the factory propose to stack the products in the factory to reduce the amount of space needed for buffering. Replace the factory process with a LIFO buffer process, run the experiments again, first with low = 0 and high = 1 and then with low = 1 and high = 4.
4. You will notice that some products stay in the factory forever. Why does that happen? How should the policy be changed to ensure all products eventually leave the factory?