Conveyors

> >

A conveyor is a long belt on which items are placed at the starting point of the conveyor. The items leave the conveyor at the end point, after traveling a certain period of time on the conveyor. The number of items traveling on the conveyor varies, while each item stays the same amount of time on the conveyor. It works like a buffer that provides output based on item arrival time instead of based on demand from the next process.

Timers

To model a conveyor, you have to wait until a particular point in time. The Chi language has timers to signal such a time-out. The timer is started by assigning it a value. From that moment, it automatically decrements when time progresses in the model, until it reaches zero. The function ready gives the boolean value true if the timer is ready. The amount of time left can be obtained by reading from the variable. An example:

proc P():
    timer t;

    delay 10.0;
    t = timer(5.0); # Get a time-out at time = 15.0
    for i in range(7):
        write("%f %f %b\n", time, real(t), ready(t));
        delay 1.0
    end
end

model M():
    run P()
end

Initially, time equals 0.0. The first action of process P is to delay the time for 10.0 time units. Now the value of time equals 10.0. Nothing happens to timer t as it was already zero. At time 10 timer t is started with the value 5.0. The output of the program is:

10.0   5.0    false
11.0   4.0    false
12.0   3.0    false
13.0   2.0    false
14.0   1.0    false
15.0   0.0    true
16.0   0.0    true

Timer t decrements as time progresses, and it is ready at 10.0 + 5.0 units. A process can have more timers active at the same moment.

A conveyor

A conveyor is schematically depicted in the following figure:

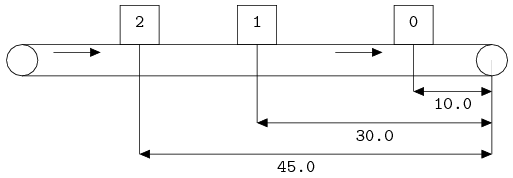
Three items are placed on the conveyor. For simplicity, assume the conveyor is 60.0 meter long and has a speed of 1 meter per second. An item thus stays on the conveyor for 60.0 seconds.

Item 0 has been placed on the conveyor 50.0 seconds ago, and will leave the conveyor 10.0 second from now. In the same way, item 1 will leave 30.0 seconds from now, and 2 leaves after 45.0 seconds. Each item has a yellow sticker with the time that the item leaves the conveyor. Based on this idea, tuple type conv_item has been defined, consisting of a field item, denoting the received item, and a timer field t, with the remaining time until the item leaves the conveyor:

type conv_item = tuple(item x; timer t);

proc T(chan? item a; chan! item b; real convey_time):
    list conv_item xst; item x;

    while true:
        select
            a?x:
                xst = xst + [(x, timer(convey_time))]
        alt
            not empty(xst) and ready(xst[0].t), b!xst[0].x:
                xst = xst[1:]
        end
    end
end

The conveyor always accepts new items from channel a, and adds the item with the yellow sticker to the list. If the conveyor is not empty, and the timer has expired for the first item in the list, it is sent (without sticker) to the next process. The conveyor sends items to a process that is always willing to a receive an item, this implies that the conveyor is never blocked. Blocking implies that the items nevertheless are transported to the end of the conveyor.

A priority conveyor

In this example, items are placed on a conveyor, where the time of an item on the conveyor varies between items. Items arriving at the conveyor process, get inserted in the list with waiting items, in ascending order of their remaining time on the conveyor. The field tt in the item denotes the traveling time of the item on the conveyor:

type item      = tuple(...; real tt; ...),
     conv_item = tuple(item x; timer t);

The predicate function pred is defined by:

func bool pred(conv_item x, y):
    return real(x.t) <= real(y.t)
end

The conveyor process becomes:

proc T(chan? item a; chan! item b):
    list conv_item xst; item x;

    while true:
        select
            a?x:
                xst = insert(xst, (x, timer(x.tt)), pred)
        alt
            not empty(xst) and ready(xst[0].t), b!xst[0].item:
                xst = xst[1:]
        end
    end
end

The conveyor process works like before, except the new item is inserted in the list according to its remaining time, instead of at the rear of the list.

Exercises

Model the system as shown in the figure below, where T is a conveyor process with a capacity of at most three products and exponentially distributed conveying times with an average of 4.0.

Compute the average flow time of products in the system.
Model the system as shown in the figure below, with exponentially distributed server processing times with an average of 4.0.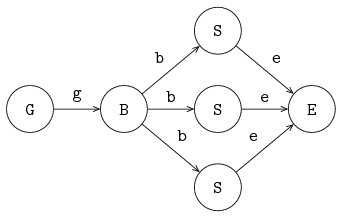
1. Compute the average flow time of products in the system.
2. Are there differences in behavior between both systems? Why (not)?