Module 1.3: Modeling discrete event systems
Discrete event systems have discrete states, with transitions between them, and the transitions are associated with events that may occur in the system. If a plant (uncontrolled system) can be seen as such a discrete event system, it can be modeled using a discrete event model. Discrete event models primarily consist of events, and of automata that have locations and edges. The models may also contain variables, and edges of automata may contain guards and updates. In this sub-module you learn more about these concepts, which are key in modeling discrete systems.
Automata, locations and edges
Discrete event systems consist of multiple parts, called components, like a bridge deck and a motor. Each component is typically modeled using a single automaton. The various automata together form the model of a system. Each state of a component is modeled as a location of the automaton, and each transition of a component is modeled as an edge of the automaton. We thus distinguish a location from a state, and an edge from a transition (more on that later).
Consider again the example from the previous sub-module, of a bridge with a bridge deck and a traffic light.
Recall that the bridge deck has three states, as it can be open, partially open or closed.
We previously named these states as deck_is_open, deck_is_partially_open and deck_is_closed.
To transition between the states, we defined three events: deck_has_opened, deck_has_become_partially_open and deck_has_closed.
For the traffic light, assuming it is a simple traffic light, it could have two states: light_signals_red and light_signals_green.
To transition between the states, we could define two events: turn_to_red and turn_to_green.
Typically, each component has an initial state.
In this case, for instance, initially the bridge deck could be closed and the traffic light could signal green, such that cars can drive over the bridge.
If we model both components separately, we would use two automata.
We could name them BridgeDeck and TrafficLight.
The three states of the bridge could then be modeled as three locations, which could be named Open, PartiallyOpen and Closed.
Because the locations are part of the BridgeDeck automaton, there is no need to repeat deck_is part of the state names.
Locations represent the states that the automaton can be in, and therefore shorter and simpler names can be used, that indicate the differences between the states.
Similarly, for the TrafficLight, we could simply name the locations Red and Green.
The Closed location would then be the initial location of the BridgeDeck automaton, and the Green location would be the initial location of the TrafficLight automaton.
Components can transition from one state (the source state) to another (the target state).
In a model, for each transition of a component the corresponding automaton contains an edge.
The edge is labeled with an event, just as a transition is associated with an event as well.
Similar to how locations can be given simpler names within the context of the automaton to which they belong, so can events.
We could for instance name the events of the bridge deck opened, partially_opened and closed.
Similarly, we could name the events of the traffic light to_red and to_green.
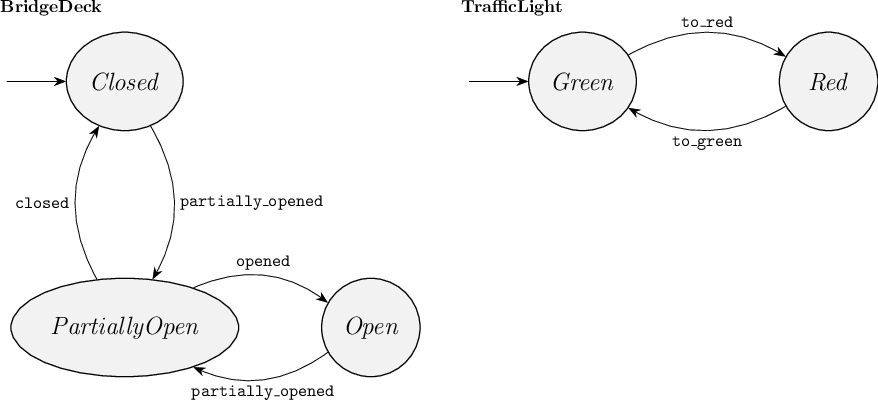
Below, you can see a graphical representation of the two automata.
Each automaton is labeled with the automaton's name.
Each location of an automaton is represented as a circle (or ellipse) that contains the name of the location.
Each edge between locations is represented as a directed arrow from its source location's circle to its target location's circle, with the name of the event being shown close to the arrow.
Multiple edges between the same locations are graphically represented by a single arrow, which is labeled with multiple event names separated with commas.
This avoids cluttering the graphical representation with many arrows.
So, for two edges labeled with events a and b, between the same source and target locations, the single arrow would be labeled with a, b.
Initial locations are indicated by an incoming arrow.
System behavior model
The state of the entire system is a combination of the states of its components, as we learned in the previous sub-module.
We can model the state space of a system also as a single automaton, that represents all the possible behavior of the system.
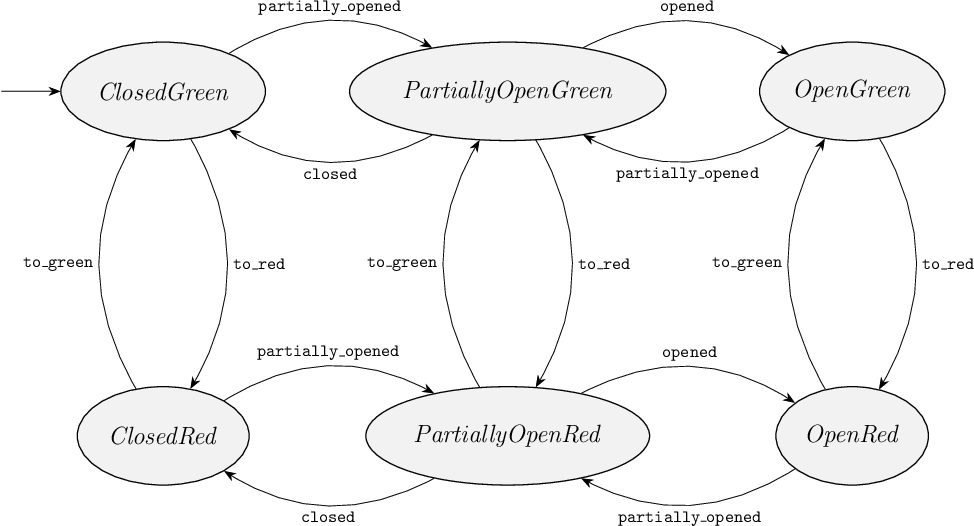
For instance, for the system consisting of a bridge deck and a traffic light, there are six states: three states of the bridge deck combined in every possible way with the two states of the traffic light.
These six states are: (deck_is_open, light_signals_red), (deck_is_open, light_signals_green), (deck_is_partially_open, light_signals_red), (deck_is_partially_open, light_signals_green), (deck_is_closed, light_signals_red) and (deck_is_closed, light_signals_green).
If we name the automaton BridgeDeckAndTrafficLight, we could simply name the states ClosedGreen, PartiallyOpenGreen, OpenGreen, ClosedRed, PartiallyOpenRed and OpenRed.
Location ClosedGreen is then the initial location.
The automaton that represents the state space of the uncontrolled system thus looks like this:
Now, let us manually derive a supervisory controller for this system.
The state space automaton represents all the behavior of the system, for both the bridge deck and the traffic light.
While all six states are physically possible, not all of them are safe for the users of the system.
For instance, in state (deck_is_partially_open, light_signals_green) a car may drive into the water if its driver is not paying attention.
For safety reasons, we must thus ensure that this state is never reached.
Therefore, a safety requirement of this system is that the traffic light may never signal green while the bridge is (partially) open.
One could argue that state (deck_is_closed, light_signals_red) is also not needed, as in that state cars are not allowed to drive over the bridge deck, while the bridge deck is closed.
From a practical point of view this does not seem like a very useful state, but it is needed for the safe operation of the system.
The operator should only be able to open the bridge while the traffic light signals red.
The traffic light should stay red while the bridge deck is opening or fully open.
Only once the bridge deck is fully closed again, may the traffic light signal green again, such that cars can safely pass over the bridge.
There is thus a brief moment, just after the bridge deck has fully closed, and just before the supervisory controller gives the traffic light the command to signal green, that the bridge deck is closed and the traffic light signals red.
Similarly, when the bridge deck is to be opened, the traffic light is first instructed to turn red, before the bridge deck is actually opened, such that again briefly the system is in the state where the bridge deck is closed and the traffic light signals red.
In general, in a discrete event system, only one event can happen at any time.
The next event could occur very quickly after the previous one, but there is thus always a state in between.
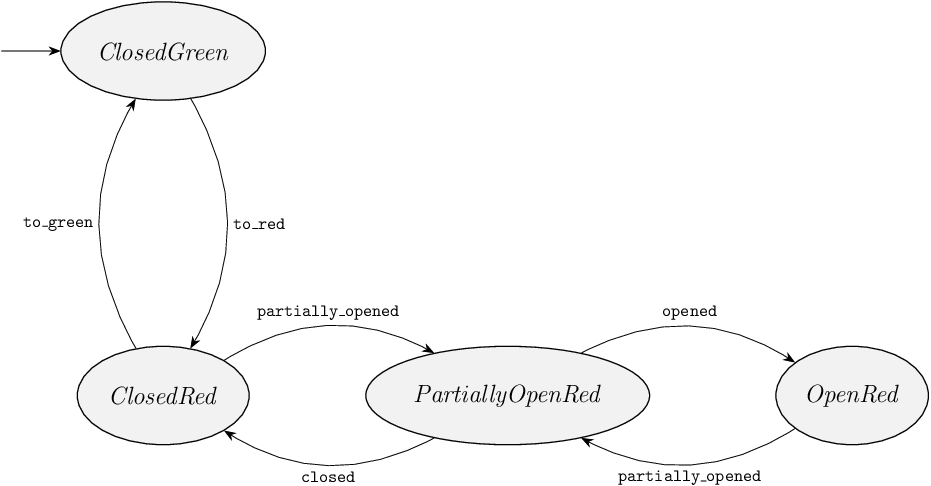
Below, the automaton representing the state space of the controlled system is shown.
It is a restricted version of the state space of the uncontrolled system.
Unsafe locations PartiallyOpenGreen and OpenGreen are removed, as are all edges to and from these locations.
There is thus no way to transition to the unsafe locations anymore, while all safe system behavior is preserved.
Variables, guards and updates
Modeling different states of a component as locations is not always convenient. Consider for instance a water lock that can accommodate at most four ships. When a fifth ship arrives, a traffic light needs to signal that the ship must wait to enter the water lock, as the water lock is full. To be able to express such behavior, the number of ships in the water lock needs to be counted. A counter can be modeled as an automaton, with for every possible number of ships a separate location. In this case, with zero, one, two, three or four ships in the water lock, that would require five locations. The counter automaton could for instance look like this:

One can imagine that the automaton becomes bigger if more ships need to be counted.
And if the number of ships changes, the automaton needs to be adapted, by adding and removing not only locations, but also all the edges between the locations.
In such a case, a variable offers a good alternative for locations, making it easier to scale and adapt the counter.
We could for instance introduce a variable named ship_count that represents the number of ships in the water lock.
Whenever a ship enters the water lock, the counter is updated by increasing the variable by one.
Similarly, whenever a ship leaves the water lock, the counter is updated by decreasing the variable by one.
Edges can have updates that indicate which variables should be updated when the edge is taken, and what their new values should become.
The simplest form of an update is an assignment that changes the value of a single variable.
It has the form v := e, where v is the variable that is to be updated, and e is an expression that when computed produces the new value of the variable.
For instance, ship_count := 2 is an assignment that assign value 2 as the new value of variable ship_count.
A bit more complicated is assignment ship_count := ship_count + 1.
It increases the value of variable ship_count by one: it takes the current value of variable ship_count and adds 1 to it, incrementing the value by one, and this incremented value is then assigned to variable ship_count.
Here variable ship_count occurs both the left and the right of the :=.
On the right, it indicates the current value of the variable, in the location from where edge starts.
On the left, it indicates the variable that is to be assigned, and that thus gets a new value in the location where the edge ends.
For our counter, we would have assignment ship_count := ship_count + 1 when event ship_enters occurs, and assignment ship_count := ship_count - 1 when event ship_leaves occurs.
A water lock can not have a negative number of ships in it.
We thus need to prevent the counter from being updated to negative values.
For this purpose, guards can be added to edges.
A guard indicates the conditions under which an edge can be taken: if the condition holds, then the edge can be taken, and if the condition does not hold, the edge can not be taken.
Conditions, such as guard conditions, are specified as predicates that can be evaluated, resulting in either true or false.
For instance, to prevent the counter from getting a negative value, we could add guard ship_count > 0 to edges for event ship_leaves.
Predicate ship_count > 0 evaluates to true if variable ship_count is larger than zero, and it evaluates to false if the variable is less than or equal to zero.
When the edge is taken, the value of the variable is still decreased by one.
But, the value of the variable always remains at least zero, since the edge can only be taken when the variable has a value larger than zero.
The guard thus disables the edge when the guard condition is not satisfied, for instance when variable ship_count has value zero.
Similarly, to count at most four ships in the water lock, guard ship_count < 4 can be added to edges for event ship_enters.
The value of the variable is then kept as such that it is at least zero and at most four.
In general, if an edge does not have an explicitly stated guard, the guard is implicitly true, a condition that always holds, meaning there is no additional restriction on when the edge can be taken.
Similar to how an automaton has an initial location, a variable has an initial value.
If initially there are no ships in the water lock, counter variable ship_count initially has value zero, which we indicate as ship_count = 0.
The alternative model of the counter, using a variable, guards and updates, could then look as follows. The initial value of the variable is indicated on the incoming arrow of the initial location. The guards and updates are shown close to the edges, with the guards being above the event name, and the updates being below it. All edges now start and end in the same single location of the automaton. Such edges, that start and end in the same location, are called self loop edges or simply self loops.

This alternative counter automaton has the same five states as the previous counter model that used five locations. In both cases, initially no ships are present in the water lock, and at most four ships can enter and be counted. In an empty water lock, a ship may thus enter four times before the lock is full and the counter reaches its maximum value. If ships leave, the counter decreases, but it never decreases beyond zero. Both models thus have the same behavior, consisting of five states and eight transitions. They are just modeled differently, using either multiple locations or a variable with multiple values. The state space of the counter automaton with the variable, represented as an automaton, is exactly that of the counter automaton modeled with locations.
Locations and variables can thus be used interchangeably to represent possible states of a component. As a modeler, you can choose whichever one is best suited for a particular situation. And more complex automata could have multiple locations and multiple variables. But an automaton always requires at least one location, while variables are optional. A state of an automaton modeled with one or more locations and zero or more variables, then consists of the current location of the automaton and the current value of each of the automaton's variables.
The locations of an automaton are called locations rather than states, as also variables can represent possible states of a component. Using different names for the concepts allows to keep them apart, and avoid confusion. Similarly, edges and transitions are different. The counter automaton with the variable has only two edges, while the state space of that automaton has eight transitions. Each edge thus corresponds to four out of the eight transitions in the state space.
It should by now be clear why a counter can better be modeled by using a variable than by using multiple locations.
The number of ships to be counted can easily be adapted by changing value 4 in guard ship_count < 4.
After all, it is much easier to change value 4 to 104 than it is to add a hundred locations and double the amount of edges.
Marked locations and states
Besides a location being an initial location, a location may also be a marked location.
By marking a location, you can indicate that you consider that location to be stable.
A sequence of events ending in a stable location can be interpreted as the completion of some tasks or operations.
Consider for instance the coffee machine from the quiz of the previous sub-module.
Initially the coffee machine is in state Waiting.
By event sequence make_choice, finish_prepare, finish_coffee and remove_cup, the coffee machine completes a full task to provide a user with a coffee.
It then returns back to stable state Waiting, where another user can again order a coffee.
An automaton should have at least one marked location, but may have multiple marked locations. A typical situation is for an automaton's initial location to also be its only marked location. For instance, components are often initially idle, then perform some task, and after performing the task they are idle again. The initial location is then a stable location, as the component is idle. In the other locations, the component is not stable, as it is busy performing its task. Another example is for instance a motor that can be turned on or off. A motor could be stable and safe when it is off, as it then doesn't drive any movements in the system, keeping the system in a stable state. Such a motor could then be modeled as an automaton with two locations, one where the motor is on, and one where the motor is off. The location where the motor is off, would be its initial and marked location, as that is where the motor is stable.
There are situations where the initial location should not be a marked location. For instance, if a component should first be calibrated or otherwise prepared before it can perform its task. The location after the calibration, where the component can repeatedly perform its task, would then be a better choice for a marked location. In such a marked location, the component is calibrated, awaiting to perform its task. And when the task is completed, it returns to its calibrated state, represented by the marked location.
Marked locations are also important when synthesizing a supervisor.
The synthesis procedure makes sure that there is always a sequence of events that leads back to a state where each automaton is in its marked location.
Marked locations can therefore be viewed as safe havens to which the system must be able to return.
For instance, the coffee machine should be able to return to its Waiting state, regardless of whether it is Preparing, MakingCoffee or Finished finished state.
The Waiting location is a safe haven that should be reachable from every location.
In the example of the bridge deck and traffic light, unsafe states PartiallyOpenGreen and OpenGreen should not be marked.
States OpenRed, PartiallyOpenRed, ClosedRed and ClosedGreen are all safe states and could be considered for marking.
One could consider a partially opened bridge deck to be less stable than a fully open or fully closed bridge deck.
And a traffic light that signals red keeps the system more stable than a traffic light that signals green, as a red signal does not allow cars to pass over the bridge.
Graphically, a marked location is represented as a circle with a double border. We come back to marking and its role in synthesis in Module 3.
In automata with both locations and variables, a marked state is a state where the current location of the automaton is a marked location and the current value of each variable is a marked value.
Often, variable value marking is left implicit, such that all values of a variable are marked values.
But, it is also possible to mark specific variable values.
Similar to specifying an initial variable value by a predicate such as ship_count = 0, we may also use a marking condition to indicate under which conditions a variable is marked.
For instance, we may indicate that a variable x is marked whether it has a value that is at least three, by using marker predicate x >= 3.
Quiz
ship_count represents the number of ships in the water lock, which is part of the system's state.",
"No: it is never possible that a variable represents the system's state, as locations are meant for this, and in the ship counter example the location with the self loop edges is the system's state."
],
correctAnswer: '1'
},
{
type: 'single-choice',
question: `
A motor that can be on or off can be modeled as an automaton with boolean variables that can be either true or false.
Which of the following is the best automaton model for this component?`,
answers: [
`Variables: off, on.Edge 1 has guard
off = true, event turn_on and update off := false.Edge 2 has guard
on = true, event turn_off and update on := false.`,
`Variables: off, on.Edge 1 has guard
off = true, event turn_on and update on := true.Edge 2 has guard
on = true, event turn_off and update off := true.`,
`Variables: off, on.Edge 1 has guard
on = false, event turn_on and update off := false.Edge 2 has guard
off = false, event turn_off and update on := false.`,
`Variables: off, on.Edge 1 has guard
on = false, event turn_on and update on := true.Edge 2 has guard
off = false, event turn_off and update off := true.`,
`Variables: on.Edge 1 has guard
on = true, event turn_on and update on := true.Edge 2 has guard
on = false, event turn_off and update on := false.`,
`Variables: on.Edge 1 has guard
on = true, event turn_on and update on := false.Edge 2 has guard
on = false, event turn_off and update on := false.`,
`Variables: on.Edge 1 has guard
on = false, event turn_on and update on := true.Edge 2 has guard
on = true, event turn_off and update on := false.`,
`Variables: on.Edge 1 has guard
on = false, event turn_on and update on := false.Edge 2 has guard
on = true, event turn_off and update on := true.`
],
correctAnswer: '7'
},
{
type: 'single-choice',
question: "What is the best definition of a marked location?",
answers: [
"It is a location that is indicated with a mark by the systems designer.",
"It is a location which the modeler of the system considers to be stable.",
"It is the location at which the automaton starts."
],
correctAnswer: '2'
},
{
type: 'single-choice',
question: `
We have an automaton Toggle that consists of the locations On and Off, representing a system that can be on or off.
Which location would you consider to be a marked location?`,
answers: [
"On, because you want your system to be on to be productive.",
"Off, because your system is safe and stable when it is off.",
"It depends on the system, as some systems have a stable On state and others a stable Off state."
],
correctAnswer: '3'
},
{
type: 'multiple-choice',
question: "Which of the following concepts can be used to model an automaton?",
answers: [
"Edges.",
"Events.",
"Guards.",
"Initial events.",
"Initial locations.",
"Marked locations.",
"Marked variable values.",
"Locations.",
"States.",
"Transitions.",
"Updates.",
"Variables.",
],
correctAnswer: '1, 2, 3, 5, 6, 7, 8, 11, 12'
},
{
type: 'single-choice',
question: `
The Toggle automaton from a previous question has initial location Off, and events go_on and go_off.
Furthermore, the automaton counts how often the system has been turned on, with the variable count that is initially zero.
The system is allowed to be turned on maximally five times for safety reasons.
The modeler of the system declared the Off location to be marked.
What is a correct automaton model for the component?`,
answers: [
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
On.
Initial values: On = 0.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count > 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and no update.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
count.
Initial values: count = 0.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count >= 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and update count := count - 1.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: On.Variables:
count.
Initial values: count = 5.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count <= 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and no update.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
On.
Initial values: On = 5.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count < 5, event go_on and update count := count - 1.Edge 2 from location
On to location Off has guard true, event go_off and no update.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
count.
Initial values: count = 0.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count < 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and no update.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
count.
Initial values: count = 0.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count <= 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and no update.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
count.
Initial values: count = 0.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count < 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and update count := count - 1.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
count.
Initial values: count = 5.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count <= 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and no update.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: Off.Variables:
count.
Initial values: count = 0.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count > 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and update count := count - 1.`,
`Locations: On, Off.
Initial locations: Off.
Marked locations: On.Variables:
count.
Initial values: count = 0.
Events: go_on, go_off.Edge 1 from location
Off to location On has guard count > 5, event go_on and update count := count + 1.Edge 2 from location
On to location Off has guard true, event go_off and no update.`
],
correctAnswer: '5'
}
];