Continuous variables
In the lesson that introduced timing, variable time was used. Variable time uses absolute model time, i.e. the total amount of time that has passed since the start of the simulation. It is usually easier to use relative model time, i.e. a certain amount of time passes after a certain event. This is where continuous variables are ideal. A continuous variable is a variable that changes value automatically, as time progresses. Consider the following CIF specification:
automaton machine:
event start, finished;
cont t = 0 der 1;
location idle:
initial;
edge start do t := 0 goto producing;
location producing:
edge finished when t >= 3 goto idle;
endThis specification models a machine that is initially idle. The machine can start to produce a product. After a while, it is done producing. Due to having finished the product, it becomes idle again, until it is starts to product the next product.
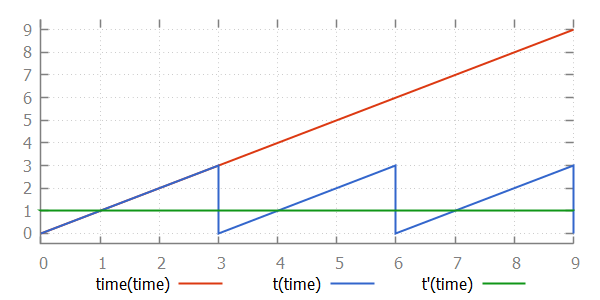
Continuous variable t is declared to initially have value 0. Its derivative is 1, meaning that every unit of time that passes, the value of t increases by 1. Every time the start event happens, the value of continuous variable t is reset to 0 using an assignment. As a result of this reset, t will be 0 when the automaton enters the producing location. The edge for the finished event indicates that the event can only happen when t >= 3 holds. This condition will hold after three time units. This means that automaton machine remains in the producing location for three time units, before going to the idle location. It will thus always take three units after entering the producing location, before the guard becomes enabled, and the finished event can take place. The state space is as follows:

The states are labeled with the first letters of the names of the current locations of automaton machine and the current values of variables time and t.
Continuous variables always have real values. Similar to discrete variables, if their initial value is not specified, it is 0.0:
cont t der 1; // Initial value is 0.0.The derivative of a continuous variable can be used as a variable as well. The derivative of continuous variable t is t'. A derivative is read only; it can not be assigned. Similar to algebraic variables, it is always equal to its definition. In the case of variable t, its derivative is always 1. The values of variables time, t, and t' as time progresses are: