Post-Training Quantization with AIDGE#

Binder

What is neural network Quantization ?#

Deploying large neural network architectures on embedded targets can be a difficult task as they often require billions of floating operations per inference.

To address this problem, several techniques have been developed over the past decades in order to reduce the computational load and energy consumption of those inferences. Those techniques include Pruning, Compression, Quantization and Distillation.

In particular, Post Training Quantization (PTQ) consists in taking an already trained network, and replacing the costly floating-point MADD by their integer counterparts. The use of Bytes instead of Floats also leads to a smaller memory bandwidth.

While this process can seem trivial, the naive approach consisting only in rounding the parameters and activations doesn’t work in practice. Instead, we want to normalize the network in order to optimize the ranges of parameters and values propagated inside the network, before applying quantization.

The Quantization Pipeline#

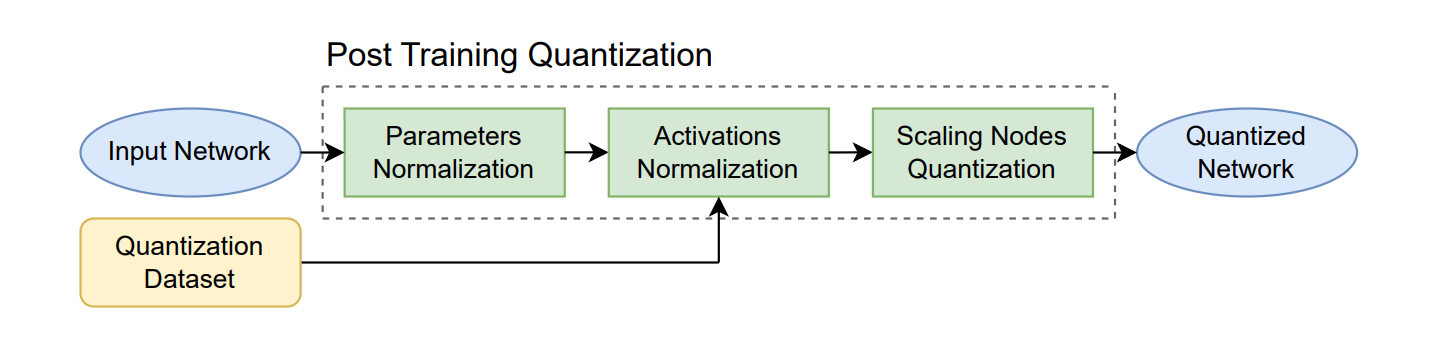
The PTQ algorithm consists of a three-steps pipeline:

  • First, we optimize the parameter ranges by propagating the scaling coefficients through the network.

  • Second, we compute the activation values over an input dataset and insert the scaling nodes.

  • Finally, we quantize the network by reconfiguring the scaling nodes according to the desired precision.

alt text

Performing PTQ with AIDGE#

This notebook shows how to perform PTQ of a convolutional neural network, trained on the MNIST dataset.

The tutorial is constructed as follows :

  • Setup of the AIDGE environment

  • Loading of the model and running example inferences

  • Evaluation of the trained model’s accuracy

  • Post-Training Quantization and test inferences

  • Evaluation of the quantized model accuracy

As we will observe in this notebook, there is zero degradation in accuracy for an 8-bit PTQ.

Environment setup#

Ensure that the Aidge modules are properly installed in the current environment. If it is the case, the following setup step can be skipped.

Note: When running this notebook on Binder, all required components are pre-installed.

[ ]:

%pip install aidge-core \
    aidge-onnx \
    aidge-backend-cpu \
    aidge-quantization

Import modules#

Besides Aidge modules, we need Numpy for manipulating the inputs, Matplotlib for visualization purposes, and gzip to uncompress the numpy dataset.

Then we want to import the Aidge modules:

  • the core module contains everything we need to manipulate the graph.

  • the backend module allows us to perform inferences using the CPU.

  • the onnx module allows us to load the pretrained model (stored in an onnx file).

  • the quantization module encaplsulate the Post Training Quantization algorithm.

[ ]:

import gzip
import numpy as np
import matplotlib.pyplot as plt

import aidge_core
import aidge_onnx
import aidge_backend_cpu
import aidge_quantization
import aidge_model_explorer

print(" Available backends : ", aidge_core.Tensor.get_available_backends())

Exploring the original ONNX Model#

Download the ONNX file and Database (if needed)#

If git-lfs is not installed, the model and data can be downloaded using the following code snippet.

Reminder: This step is not needed when running in Binder.

[ ]:

BASE_URL = "https://gitlab.eclipse.org/eclipse/aidge/aidge/-/raw/main/examples/tutorials/PTQ_tutorial/"

# Download the model, input and output data files
files_to_download = ["ConvNet.onnx", "mnist_samples.npy.gz", "mnist_labels.npy.gz"]

for file_name in files_to_download:
    aidge_core.utils.download_file(
        file_path=file_name, file_url=f"{BASE_URL}{file_name}"
    )

Setup variables and Database visualization#

Then, let’s define the configurations of this script …

[ ]:

NB_SAMPLES = 100

Now, let’s load and visualize some samples:

[ ]:

samples = np.load(gzip.GzipFile("mnist_samples.npy.gz", "r"))
labels = np.load(gzip.GzipFile("mnist_labels.npy.gz", "r"))

[ ]:

for i in range(10):
    plt.subplot(1, 10, i + 1)
    plt.axis("off")
    plt.tight_layout()
    plt.imshow(samples[i], cmap="gray")

Importing the model in Aidge#

[ ]:

aidge_model = aidge_onnx.load_onnx("ConvNet.onnx", verbose=False)
aidge_core.remove_flatten(aidge_model)  # we want to get rid of the 'flatten' nodes ...

Setting up the Aidge Scheduler#

In order to perform inferences with Aidge we need to setup a Scheduler. But before doing so, we need to create a data producer node and connect it to the network.

[ ]:

# Set up the backend
aidge_model.set_datatype(aidge_core.dtype.float32)
aidge_model.set_backend("cpu")

# Create the Scheduler
scheduler = aidge_core.SequentialScheduler(aidge_model)

Running some example inferences#

Now that the scheduler is ready, let’s perform some inferences. To do so we first declare a utility function that will prepare and set our inputs, propagate them and retreive the outputs.

[ ]:

def propagate(model, scheduler, sample):
    # Setup the input
    sample = np.reshape(sample, (1, 1, 28, 28))
    input_tensor = aidge_core.Tensor(sample)
    # Run the inference
    scheduler.forward(True, [input_tensor])
    # Gather the results
    output_node = model.get_ordered_outputs()[0][0]
    output_tensor = output_node.get_operator().get_output(0)
    return np.array(output_tensor)


print("\n EXAMPLE INFERENCES :")
for i in range(10):
    output_array = propagate(aidge_model, scheduler, samples[i])
    print(labels[i], " -> ", np.round(output_array, 2))

Computing the original model accuracy#

[ ]:

def compute_accuracy(model, samples, labels):
    acc = 0
    for i, x in enumerate(samples):
        y = propagate(model, scheduler, x)
        if labels[i] == np.argmax(y):
            acc += 1
    return acc / len(samples)


accuracy = compute_accuracy(aidge_model, samples[0:NB_SAMPLES], labels)
print(f"\n MODEL ACCURACY : {accuracy * 100:.3f}%")

Model Visualization Before PTQ#

Before performing PTQ, it is useful to visualize the model.
For this, we use aidge_model_explorer, which displays the model as a graph in the browser.
[ ]:

aidge_model_explorer.visualize(aidge_model, "model_before_ptq")

Quantization dataset creation#

We need to convert a subset of our Numpy samples into Aidge tensors, so that they can be used to compute the activation ranges.

[ ]:

tensors = []
for sample in samples[0:NB_SAMPLES]:
    sample = np.reshape(sample, (1, 1, 28, 28))
    tensor = aidge_core.Tensor(sample)
    tensors.append(tensor)

Graph Annotation Before PTQ#

The last step before invoking PTQ is to annotate the graph to specify the desired precision.

There are two possible approaches:

1. Manual Annotation#

The user can manually annotate the graph by adding the dynamic attributes:

  • quantization.ptq.precision

  • quantization.ptq.accumulationprecision

to each node in the graph.

⚠️ This method can be tedious and prone to errors.

2. Automatic Annotation#

Alternatively, the user can use the function auto_assign_node_precision() which automatically assigns the desired precisions across the entire graph.

It takes as arguments the target precisions for:

  • Weights

  • Activations

  • Accumulations & Biases

Finally, we still need to define the number of bits for quantizing the model (to properly quantize the inputs) in accordance with the data types selected in the auto_assign_node_precision() function.

[ ]:

NB_BITS = 4
weight_precision = aidge_core.dtype.int4
activation_precision = aidge_core.dtype.int4
bias_and_accumulation_precision = (
    aidge_core.dtype.int16
)  # The precision for the accumulation must always be greater

aidge_quantization.auto_assign_node_precision(
    aidge_model, weight_precision, activation_precision, bias_and_accumulation_precision
)

Applying PTQ to the model#

With the setup complete, we can run the PTQ routine.

Note: after quantization, the scheduler must be updated.

[ ]:

aidge_quantization.quantize_network(
    network=aidge_model,  # The AIDGE model to quantize
    calibration_set=tensors,  # Calibration dataset used to estimate useful value ranges
    clipping_mode=aidge_quantization.Clipping.MSE,  # Clipping method applied (e.g., MSE clipping)
    no_quant=False,  # Debug flag; disables quantization rounding if True to avoid data loss
    optimize_signs=False,  # Sign optimization: can improve post-quantization accuracy
    # by detecting purely unsigned ranges and exploiting them
    single_shift=False,  # Single Shift Approximation:
    # replaces floating-point multiplications with bit shifts
    # Note: only effective for integer target types
    use_cuda=False,  # Enable CUDA for faster range computation during PTQ
    fold_graph=True,  # Apply constant folding to merge quantizers with their producers
    # Reduces graph size and improves efficiency
    fake_quantize=True,  # If True, does not cast tensors to the target datatype
    # Graph stays in float (useful for testing or simulation)
    verbose=False,  # Enable verbose logging
)


scheduler = aidge_core.SequentialScheduler(aidge_model)
We can now visualize our quantized model!
Since the fake_quantize argument was not enabled, the model has been cast to the desired target type.
[ ]:

aidge_model_explorer.visualize(aidge_model, "model_after_PTQ")

Performing inference with the quantized network#

Now that the network has been quantized, it’s time to evaluate it by running inference. Before doing so, remember that the 8-bit network expects 8-bit inputs. We therefore need to rescale the input tensors accordingly.

[ ]:

scaling = 2 ** (NB_BITS - 1) - 1
for i in range(NB_SAMPLES):
    samples[i] = np.round(samples[i] * scaling)

We can now perform inference using the quantized model.

[ ]:

print("\n EXAMPLE QUANTIZED INFERENCES :")
for i in range(10):
    input_array = np.reshape(samples[i], (1, 1, 28, 28))
    output_array = propagate(aidge_model, scheduler, input_array)
    print(labels[i], " -> ", np.round(output_array, 2))

Evaluating the accuracy of the quantized model#

As with the original network, we now compute the quantized model’s accuracy:

[ ]:

accuracy = compute_accuracy(aidge_model, samples[0:NB_SAMPLES], labels)
print(f"\n QUANTIZED MODEL ACCURACY : {accuracy * 100:.3f}%")

What is Fake Quantization and Why It Matters#

When applying Post-Training Quantization (PTQ), the goal is to represent the model’s weights and activations using fewer bits (e.g., 8-bit integers instead of 32-bit floats).
However, during experimentation, we often want to simulate quantization behavior without actually changing the tensor data types.
This is where fake quantization comes in.
Fake quantization (also called quantization simulation) emulates the effects of low-bit quantization while keeping all computations in floating-point.
In practice, each tensor is:

  1. Clamped to the quantization range (e.g., [-128, 127] for int8)

  2. Rounded to the nearest representable integer level

This process allows you to:

  • Evaluate quantization effects on model accuracy before implementing integer kernels

  • Debug quantization errors while keeping the model in a safe float environment

  • Train or fine-tune models with quantization awareness (QAT)

  • Ensure consistency between simulated and real integer inference

In summary, fake quantization is essential for experimenting with new bit widths (such as 4-bit or even lower) and verifying that your quantization scheme preserves model performance, all without requiring specific integer operator implementations.

You can now experiment by changing the number of bits used for quantization.
However, to do this correctly, several values must be adjusted:

  1. Set ``NB_BITS`` to the desired value (e.g., 4 for 4-bit quantization) to properly quantize the inputs on that bit width.

  2. Adapt the node auto-tagging routine to match the new bit width:

    • weight_precision = aidge_core.dtype.int4

    • activation_precision = aidge_core.dtype.int4

    • bias_and_accumulation_precision = aidge_core.dtype.int16

  3. Execute PTQ: The model can now be quantized to 4 bits.

Note: this does not mean that operator kernels are actually implemented for 4-bit integers in our backend.
To avoid errors, set fake_quantize=True to keep the model in its original data type (e.g., float) and simulate 4-bit quantization instead. When running the export if 4-bit is supported by the targeted hardware, the model will run with this precision. Otherwise Aidge support bit unpacking logic to store 4-bit information in 32-bit, resulting in slower inference but with the benefit of reducing the memory footprint of the weight and activations.

Task completed!#

We observe that 8-bit Post-Training Quantization does not degrade the model’s accuracy. This result demonstrates that a well-designed quantization algorithm can enable the deployment of neural networks on resource-constrained devices, where operating with bytes is optimal.Feel free to experiment by re-running this notebook with even more aggressive quantization settings!