Expressions
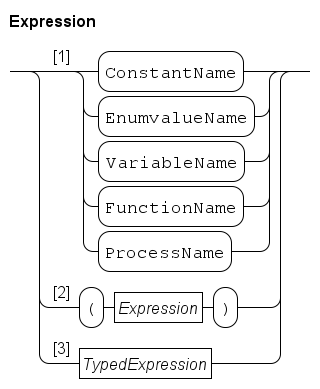
Expressions are computations to obtain a value. The generic syntax of an expression is shown below.
-
As shown in Path 1, a name may be used in an expression. It must refer to a value that can be used in an expression. Names are explained further at Names.
The first four entries are quite normal, function names can be used for variables with a function type (see Function type) and process names for variables with a process type (see Process type). The latter two are mainly useful as actual parameters of functions or processes.
-
Path 2 states that you can write parentheses around an expression. Its main use is to force a different order of applying the unary and binary operators (see Operator priorities). Parentheses may also be used to clarify the meaning of a complicated expression.
-
Path 3 gives access to the other parts of expressions. Typed expressions gives the details about typed expressions.
Typed expressions
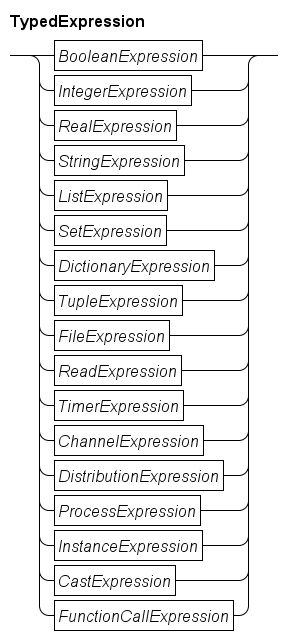
The number of operators in expressions is quite large. Also, each node has an associated type, and the allowed operators depend heavily on the types of the sub-expressions. To make expressions easier to access, they have been split. If possible the (result) type is leading, but in some cases (like the ReadExpression for example) this is not feasible.
-
The expressions with a boolean type are denoted by the
BooleanExpressionblock and explained further in Boolean expressions. -
The expressions with an integer type are denoted by the
IntegerExpressionblock and explained further in Integer expressions. -
The expressions with a real number type are denoted by the
RealExpressionblock and explained further in Real number expressions. -
The expressions with a string type are denoted by the
StringExpressionblock and explained further in String expressions. -
The expressions with a list type are denoted by the
ListExpressionblock and explained further in String expressions. -
The expressions with a set type are denoted by the
SetExpressionblock and explained further in Set expressions. -
The expressions with a dictionary type are denoted by the
DictionaryExpressionblock and explained further in Dictionary expressions. -
The expressions with a tuple type are denoted by the
TupleExpressionblock and explained further in Tuple expression. -
The expressions with a file handle type are denoted by the
FileExpressionblock and explained further in File handle expressions. -
The function to read values from an external source is shown in the
ReadExpressionblock, and further discussed in Read expression. -
The expressions with a timer type are denoted by the
TimerExpressionblock and explained further in Timer expressions. -
The expressions with a channel type are denoted by the
ChannelExpressionblock and explained further in Channel expressions. -
The expressions with a distribution type are denoted by the
DistributionExpressionblock and explained further in Distribution expressions. -
The expressions with a process type are denoted by the
ProcessExpressionblock and explained further in Process expressions. -
The expressions with an instance type are denoted by the
InstanceExpressionblock and explained further in Instance expressions. -
The expressions that convert one type to another are denoted by the
CastExpressionblock, and explained further in Cast expressions. -
The expressions that perform a function call are denoted by the
FunctionCallExpressionblock, and explained further in Function call expressions.
Enumeration value
Enumeration values may be used as literal value in an expression.

See Enumeration definitions for a discussion about enumeration definitions and enumeration values.
There are two binary operators for enumeration values.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
E |
E |
bool |
Test for equality |
|
lhs |
E |
E |
bool |
Test for inequality |
Two enumeration values from the same enumeration definition E can be compared against each other for equality (or in-equality). Example:
enum FlagColours = {red, white, blue};
...
bool same = (red == white);Boolean expressions
The literal values for the boolean data type are as follows.
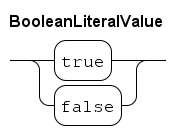
The values true and false are also the only available values of the boolean data type.
The not operation is the only boolean unary operator.
| Expression | Type op | Type result | Explanation |
|---|---|---|---|
|
|
bool |
bool |
op value is inverted. |
The and, the or, and the equality tests are available for boolean values.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
bool |
bool |
bool |
Both operands hold |
|
lhs |
bool |
bool |
bool |
At least one operand holds |
|
lhs |
bool |
bool |
bool |
Test for equality |
|
lhs |
bool |
bool |
bool |
Test for inequality |
Integer expressions
The syntax of an integer literal number is (at character level) as follows.
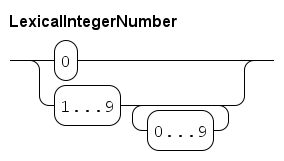
| This diagram works at lexical level (at the level of single characters), white space or comments are not allowed between elements in this diagram. |
An integer number is either 0, or a sequence of decimal digits, starting with a non-zero digit.
There are two unary operators on integer numbers.
| Expression | Type op | Type result | Explanation |
|---|---|---|---|
|
|
int |
int |
op value is negated. |
|
|
int |
int |
op value is copied. |
With the unary - operation, the sign of the operand gets toggled. The + unary operation simply copies its argument.
There are many binary operations for integer numbers, see the table below.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
int |
int |
int |
Integer addition |
|
lhs |
int |
int |
int |
Integer subtraction |
|
lhs |
int |
int |
int |
Integer multiplication |
|
lhs |
int |
int |
real |
Real division |
|
lhs |
int |
int |
int |
Integer divide operation |
|
lhs |
int |
int |
int |
Modulo operation |
|
lhs |
int |
int |
real |
Power operation |
|
lhs |
int |
int |
bool |
Test for less than |
|
lhs |
int |
int |
bool |
Test for less or equal |
|
lhs |
int |
int |
bool |
Test for equality |
|
lhs |
int |
int |
bool |
Test for inequality |
|
lhs |
int |
int |
bool |
Test for bigger or equal |
|
lhs |
int |
int |
bool |
Test for bigger than |
The divide operator / and the power operator ^ always gives a real result, integer division is performed with div. The operation always rounds down, that is a div b == floor(a / b) for all integer values a and b. The mod operation returns the remainder from the div, that is a mod b == a - b * (a div b). The table below gives examples. For clarity, the sign of the numbers is explicitly added everywhere.
| Example | Result | Explanation |
|---|---|---|
|
|
+1 |
|
|
|
+3 |
|
|
|
-2 |
|
|
|
-1 |
|
|
|
-2 |
|
|
|
+1 |
|
|
|
+1 |
|
|
|
-3 |
|
The Chi simulator uses 32 bit integer variables, which means that only values from -2,147,483,647 to 2,147,483,647 (with an inclusive upper bound) can be used. Using a value outside the valid range will yield invalid results. Sometimes such values are detected and reported.
| The technical minimum value for integers is -2,147,483,648, but this number cannot be entered as literal value due to parser limitations. |
Real number expressions
Real numbers are an important means to express values in the contiguous domain. The type of a real number expression is a real type, see Real type for more information about the type. The syntax of real number values is as follows.
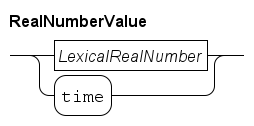
There are two ways to construct real numbers, by writing a literal real number, or by using time which returns the current time in the model.
The syntax of a literal real number (at character level) is as follows.
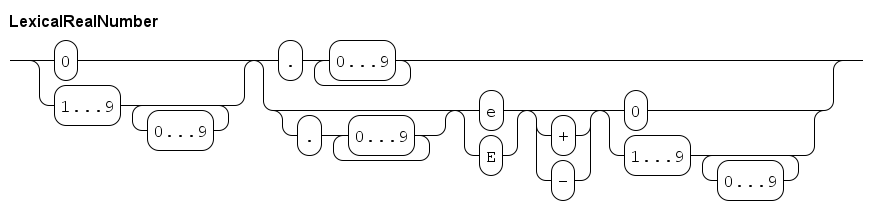
| This diagram works at lexical level (at the level of single characters), white space or comments are not allowed between elements in this diagram. |
A literal real number starts with one or more digits, and then either a dot or an exponent. In the former case, an exponent is allowed as well. Examples:
3.14
0.314e1
314E-2A real number always has either a dot character, or an exponent notation in the number.
Many of the integer operations can also be performed on real numbers. The unary operators are the same, except for the type of the argument.
| Expression | Type op | Type result | Explanation |
|---|---|---|---|
|
|
real |
real |
op value is negated. |
|
|
real |
real |
op value is copied. |
With the unary - operation, the sign of the operand gets toggled. The + unary operation simply copies its argument.
The binary operators on real numbers is almost the same as the binary operators on integer numbers. Only the div and mod operations are not here.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
int,real |
int,real |
real |
Addition |
|
lhs |
int,real |
int,real |
real |
Subtraction |
|
lhs |
int,real |
int,real |
real |
Multiplication |
|
lhs |
int,real |
int,real |
real |
Real division |
|
lhs |
int,real |
int,real |
real |
Power operation |
|
lhs |
int,real |
int,real |
bool |
Test for less than |
|
lhs |
int,real |
int,real |
bool |
Test for less or equal |
|
lhs |
int,real |
int,real |
bool |
Test for equality |
|
lhs |
int,real |
int,real |
bool |
Test for inequality |
|
lhs |
int,real |
int,real |
bool |
Test for bigger or equal |
|
lhs |
int,real |
int,real |
bool |
Test for bigger than |
With these operations, one of the operands has to be a real number value, while the other operand can be either an integer value or a real number value.
The standard library functions for real numbers contain a lot of math functions. They can be found in Real number functions.
The Chi simulator uses 64-bit IEEE 754 floating point numbers to represent real number values. Using a value outside the valid range of this format will yield invalid results. Sometimes such values are detected and reported.
String expressions
Strings are sequences of characters. Their most frequent use is to construct text to output to the screen. A string literal is defined as follows.
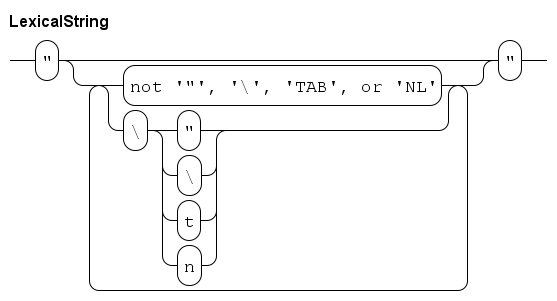
| This diagram works at lexical level (at the level of single characters), white space or comments are not allowed between elements in this diagram. |
A string literal starts with a quote character ", and ends with another quote character. In between, you may have a sequence of characters. Most characters can be written literally (eg write a a to get an 'a' in the string). The exceptions are a backslash \, a quote ", a TAB, and a NL (newline) character. For those characters, write a backslash, followed by \, ", t, or n respectively. (A TAB character moves the cursor to the next multiple of 8 positions at a line, a NL moves the cursor to the start of the next line.)
Strings have the following binary expressions.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
string |
string |
string |
Concatenation |
|
lhs |
string |
int |
string |
Element access |
|
lhs |
string |
int, int |
string |
Slicing with step |
|
lhs |
string |
int, int, int |
string |
Slicing |
|
lhs |
string |
string |
bool |
Test for less than |
|
lhs |
string |
string |
bool |
Test for less or equal |
|
lhs |
string |
string |
bool |
Test for equality |
|
lhs |
string |
string |
bool |
Test for inequality |
|
lhs |
string |
string |
bool |
Test for bigger or equal |
|
lhs |
string |
string |
bool |
Test for bigger than |
The concatenation operator joins two strings ("a" + "bc" gives "abc").
The element access and slicing operators use numeric indices to denote a character in the string. First character has index value 0, second character has index 1, and so on. Negative indices count from the back of the string, for example index value -1 points to the last character of a string. Unlike lists, both the element access and the slicing operators return a string. The former constructs a string with only the indicated character, while the latter constructs a sub-string where the first character is at index low, the second character at index low + step, and so on, until index value high is reached or crossed. That final character is not included in the result (that it, the high boundary is excluded from the result). If low is omitted, it is 0, if high is omitted, it is the length of the string (size( lhs )). If step is omitted, it is 1. A few examples:
string s = "abcdef";
s[4] # results in "e"
s[2:4] # results in "cd"
s[1::2] # results in "bdf"
s[-1:0:-2] # results in "fdb"
s[-1:-7:-1] # results in "fedcba"
s[:4] # results in "abcd"
s[-1:] # results in "f" (from the last character to the end)In the comparison operations, strings use lexicographical order.
There are also a few standard library functions on strings, see String functions for details.
Note that length of the string is not the same as the number of characters needed for writing the string literal, as shown in the following example.
size("a") # results in 1, string is 1 character long (namely 'a').
size("\n") # results in 1, string contains one NL character.List expressions
Lists are very versatile data structures, the Chi language has a large number of operations and functions for them.
The most elementary list expression is a literal list. It has the following syntax.
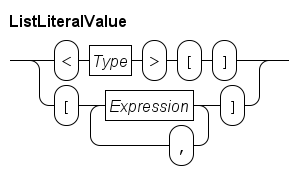
The first line shows the syntax of an empty list. The Type block denotes the element type of the list, for example <int>[] is an empty list of integer values.
The second line shows how to write a non-empty literal list value. It is a comma-separated sequence of expressions surrounded by square brackets. The type of all expressions must be the same, and this is also the element type of the list.
Some examples:
list int xs;
list int ys = <int>[];
list int zs = [1, 4, 28];Variable ys is assigned an empty list with integer element type. Since an empty list is the default value of a variable, xs has the same value. Variable zs is initialized with a list holding three elements.
Two list values are equal when they have the same number of element values, and each value is pair-wise equal.
Lists have no unary operators, the binary operators of lists are shown below.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
list T |
int |
T |
Element access |
|
lhs |
list T |
int, int |
list T |
Slicing with step |
|
lhs |
list T |
int, int, int |
list T |
Slicing |
|
lhs |
list T |
list T |
list T |
Concatenation |
|
lhs |
list T |
list T |
list T |
List subtraction |
|
lhs |
list T |
list T |
bool |
Test for equality |
|
lhs |
list T |
list T |
bool |
Test for inequality |
|
lhs |
T |
list T |
bool |
Element test |
The element access operator 'lhs [ rhs ] ' indexes with zero-based positions, for example xs[0] retrieves the first element value, xs[1] retrieves the second value, etc. Negative indices count from the back of the list, xs[-1] retrieves the last element of the list (that is, xs[size(xs)-1]), xs[-2] gets the second to last element, ect. It is not allowed to index positions that do not exist. Examples:
list int xs = [4, 7, 18];
int x;
x = xs[0]; # assigns 4
x = xs[2]; # assigns 18
x = xs[-1]; # assigns 18
x = xs[-2]; # assigns 7
xs[2] # ERROR, OUT OF BOUNDS
xs[-4] # ERROR, OUT OF BOUNDSThe slicing operator 'lhs [ low : high ] ' extracts (sub-)lists from the lhs source. The low and high index expressions may be omitted (and default to 0 respectively size( lhs ) in that case). As with element access, negative indices count from the back of the list. The result is the list of values starting at index low, and up to but not including the index high. If the low value is higher or equal to high, the resulting list is empty. For example:
list int xs = [4, 7, 18];
list int ys;
ys = xs[0:2]; # assigns [4, 7]
ys = xs[:2]; # == xs[0:2]
ys = xs[1:]; # == xs[1:3], assigns [7, 18]
ys = xs[:]; # == xs[0:3] == xs
ys = xs[1:2]; # assigns [7] (note, it is a list!)
ys = xs[0:0]; # assigns <int>[]
ys = xs[2:1]; # assigns <int>[], lower bound too high
ys = xs[0:-1]; # == xs[0:2]The slicing operator with the step expression (that is, the expression with the form 'lhs [ low : high : step ] ') can also skip elements (with step values other than 1) and traverse lists from back to front (with negative step values). Omitting the step expression or using 0 as its value, uses the step value 1. This extended form does not count from the back of the list for negative indices, since the high value may need to be negative with a negative step size.
The first element of the result is at 'lhs [low ]'. The second element is at 'lhs [low + step ]', the third element at 'lhs [low + 2 * step ]' and so on. For a positive step value, the index of the last element is the highest value less than high, for a negative step value, the last element is the smallest index bigger than high (that is, boundary high is excluded from the result). The (sub-)list is empty when the first value ('lhs [ low ]') already violates the conditions of the high boundary.
Examples:
list int xs = [4, 7, 18];
list int ys;
ys = xs[::2]; # == xs[0:3:2], assigns [4, 18]
ys = xs[::-1]; # == xs[2:-1:-1], assigns [18, 7, 4]With the latter example, note that the -1 end value in xs[2:-1:-1] really means index -1, it is not rewritten!
The concatenation operator + 'glues' two lists together by constructing a new list, copying the value of the lhs list, and appending the values of the rhs:
[1, 2] + [3, 4] == [1, 2, 3, 4]
<int>[] + [1] == [1]
[5] + <int>[] == [5]The subtraction operator - subtracts two lists. It copies the lhs list, and each element in the rhs list is searched in the copy, and the left-most equal value is deleted. Searched values that do not exist are silently ignored. The result of the operation has the same type as the lhs list. Some examples:
[1, 2, 4, 2] - [4] # results in [1, 2, 2], 4 is removed.
[1, 2, 4, 2] - [6] # results in [1, 2, 4 2], 6 does not exist.
[1, 2, 4, 2] - [1, 4] # results in [2, 2], 1 and 4 are removed.
[1, 2, 4, 2] - [2] # results in [1, 4, 2], first 2 is removed.
[1, 2, 4, 2] - [2, 2] # results in [1, 4].
[1, 2, 4, 2] - [2, 2, 2] # results in [1, 4], no match for the 3rd '2'.The element test operator in tests whether the value lhs exists in list rhs. This operation is expensive to compute, if you need this operation frequently, consider using a set instead. Some examples of the element test operation:
1 in [1, 2, 3] == true
4 in [1, 2, 3] == false # there is no 4 in [1, 2, 3]
[1] in [[2], [1]] == true
[2, 1] in [[1, 2]] == false # [2, 1] != [1, 2]
<int>[] in <list int>[] == false # empty list contains no values.There are also standard library functions for lists, see List functions for details.
Set expressions
Literal sets are written as follows.
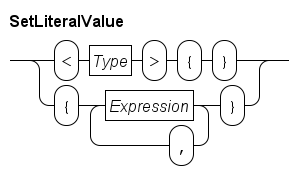
The first line shows the syntax of an empty set. The Type block denotes the element type of the set, for example <int>{} is an empty set of integer values.
The second line shows how to write a non-empty literal set value. It is a comma-separated sequence of expressions surrounded by curly brackets. The type of all expressions must be the same, and this is also the element type of the set. The order of the values in the literal is not relevant, and duplicate values are silently discarded. For example:
set real xr = {1.0, 2.5, -31.28, 1.0}assigns the set {-31.28, 1.0, 2.5} (any permutation of the values is allowed). By convention, elements are written in increasing order in this document.
Two set values are equal when they have the same number of element values contained, and each value of one set is also in the other set. The order of the elements in a set is not relevant, any permutation is equivalent.
Like lists, sets have no unary operators. They do have binary operators though. The operators are as follows.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
set T |
set T |
set T |
Set union |
|
lhs |
set T |
set T |
set T |
Set difference |
|
lhs |
set T |
set T |
set T |
Set intersection |
|
lhs |
set T |
set T |
bool |
Test for equality |
|
lhs |
set T |
set T |
bool |
Test for inequality |
|
lhs |
T |
set T |
bool |
Element test |
|
lhs |
set T |
set T |
bool |
Sub-set test |
The union of two sets means that the lhs elements and the rhs elements are merged into one set (and duplicates are silently discarded). Set difference makes a copy of the lhs set, and removes all elements that are also in the rhs operand. The result of the operation has the same type as the lhs set. Set intersection works the other way around, its result is a set with elements that exist both in lhs and in rhs. Some examples:
set int xr = {1, 3, 7};
set int yr;
yr = xr + {1, 2}; # assigns {1, 2, 3, 7}
yr = xs - {1, 2}; # assigns {3, 7}
yr = xs * {1, 2}; # assigns {1}The element test of sets tests whether the value lhs is an element in the set rhs. This operation is very fast. The sub-set test does the same for every element value in the lhs operand. It returns true is every value of the left set is also in the right set. A few examples:
1 in {1, 3, 7} == true
9 in {1, 3, 7} == false
{1} sub {1, 3, 7} == true
{9} sub {1, 3, 7} == false
{1, 9} sub {1, 3, 7} == false # All elements must be present.
{1, 3, 7} sub {1, 3, 7} == true # All sets are a sub-set of themselves.There are also standard library functions for sets, see Set functions for details.
Dictionary expressions
Literal dictionaries are written using the syntax shown below.
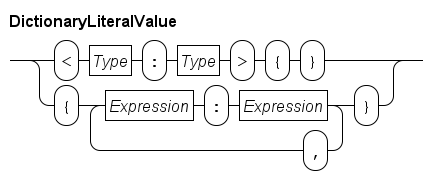
An empty dictionary needs the key and value type prefix, for example <string:int>{} is an empty dictionary with strings as key, and integer numbers as value. Literal values of such a dictionary are:
dict(string, int) d; # Initialized with the empty dictionary.
d = {"one": 1, "twenty-three": 23};The key-value pairs can be put in any order. Also, the key value must be unique. Two dictionaries are equal when they have the same number of keys, each key in one dictionary is also in the other dictionary, and the value associated with each key also match pair-wise.
The binary operators of dictionaries are as follows.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
dict(K:V) |
K |
V |
Element access |
|
lhs |
dict(K:V) |
dict(K:V) |
dict(K:V) |
Update |
|
lhs |
dict(K:V) |
dict(K:V) |
dict(K:V) |
Subtraction |
|
lhs |
dict(K:V) |
list K |
dict(K:V) |
Subtraction |
|
lhs |
dict(K:V) |
set K |
dict(K:V) |
Subtraction |
|
lhs |
dict(K:V) |
dict(K:V) |
bool |
Test for equality |
|
lhs |
dict(K:V) |
dict(K:V) |
bool |
Test for inequality |
|
lhs |
K |
dict(K:V) |
bool |
Element test |
|
lhs |
dict(K:V) |
dict(K:V) |
bool |
Sub-set test |
The element access operator accesses the value of a key. Querying the value of a non-existing key value is not allowed, however when used at the left side of an assignment, it acts as an adding operation. A few examples:
dict(int:bool) d = {1:true, 2:false};
bool b;
b = d[1]; # assigns 'true' (the value of key 1).
d[1] = false; # updates the value of key '1' to 'false'.
d[8] = true; # adds pair 8:true to the dictionary.The + operation on dictionaries is an update operation. It copies the lhs dictionary, and assigns each key-value pair of the rhs dictionary to the copy, overwriting values copied from the lhs. For example:
dict(int:bool) d = {1:true, 2:false};
d + {1:false} # result is {1:false, 2:false}
d + {3:false} # result is {1:true, 2:false, 3:false}The subtraction operator only takes keys into consideration, that is, it makes a copy of the lhs dictionary, and removes key-value pairs where the key is also in the rhs argument (for subtraction of lists and sets, the elements are used, instead of the keys):
dict(int:bool) d = {1:true, 2:false};
d - {1:false} # results in {2:false}, value of '1' is not relevant
d - [1] # results in {2:false}
d - {1} # results in {2:false}As with list subtraction and set difference, the type of the result is the same as the type of the lhs dictionary.
The element test tests for presence of a key value, and the sub-set operation tests whether all keys of the lhs value are also in the rhs value. Examples:
dict(int:bool) d = {1:true, 2:false};
bool b;
b = 2 in d; # assigns 'true', 2 is a key in d.
b = 5 in d; # assigns 'false', 5 is not a key in d.
{1:false} sub d # results in 'true', all keys are in d.There are also standard library functions for dictionaries, see Dictionary functions for details.
Tuple expression
A tuple expression is a value of a tuple type (explained in Tuple type). A tuple expression literal value is written as shown below.
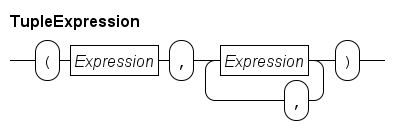
A literal tuple is a comma separated sequence of expressions of length two or longer, surrounded by a pair of parentheses. The number of expressions and the type of each expression decide the tuple type. For example:
type tup = tuple(bool b; real r);
tup t = (true, 3.48);The type named tup is a tuple type with a boolean field and a real field. The expression (true, 3.48) constructs the same tuple type, thus it can be assigned to variable t. Names of the fields are not relevant in this matching, for example variable declaration (and initialization) tuple(bool z; real w) u = t is allowed, since the types of the fields match in a pair-wise manner.
A field of a tuple can be accessed both for read and for assignment by the name of the field:
bool c;
c = t.b; # Read the 'b' field.
t.b = false; # Assign a new value to the 'b' field.In the latter case, only the assigned field changes, all other fields keep the same value.
Tuples can also be packed and unpacked. Packing is assignment to all fields, while unpacking is reading of all fields into separate variables:
real q;
t = false, 3.8; # Packing of values into a tuple.
c, q = t; # Unpacking into separate variables.Packing is very closely related to literal tuples above. The difference is that packing can be done only like above in an assignment to a tuple value, while a literal tuple works everywhere.
Unpacking is very useful when the right side (t in the example) is more complex, for example, the return value of a function call, as in c, q = f();. In such cases you don’t need to construct an intermediate tuple variable.
Packing and unpacking is also used in multi-assignment statements:
a, b = 3, 4; # Assign 3 to 'a', and 4 to 'b'.
a, b = b, a; # Swap values of 'a' and 'b'.The latter works due to the intermediate tuple that is created as part in the assignment.
File handle expressions
Variables of type file are created using a variable declaration with a file type, see File type for details about the type.
You cannot write a literal value for a file type (nor can you read or write values of this type), file values are created by means of the open function in the standard library, see File functions.
You can test whether two files are the same with the binary == and != operators.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
file |
file |
bool |
Test for equality |
|
lhs |
file |
file |
bool |
Test for inequality |
Values of type file are used for writing output to a file using the Write statement, or for reading values from a file using the read function explained in Read expression. After use, a file should be closed with a close statement explained at Close statement.
Read expression
The read expression reads a value of a given type from the keyboard or from a file. It has two forms:
-
Tread(T) -
Read a value of type
Tfrom the keyboard. -
Tread(file f, T) -
Read a value of type
Tfrom the file opened for reading by filef(see theopenfunction in File functions for details about opening files).
You can read values from types that contain data used for calculation, that is values of types bool, int, real, string, list T, set T, and dict(K:V). Types T, K, and V must also be readable types of data (that is, get chosen from the above list of types).
Reading a value takes a text (with the same syntax as Chi literal values of the same type), and converts it into a value that can be manipulated in the Chi model. Values read from the text have to be constant, for example the input time cannot be interpreted as real number with the same value as the current simulation time.
Timer expressions
Timers are clocks that count down to 0. They are used to track the amount of time you still have to wait. Timers can be stored in data of type timer (see Timer type for details of the type).
The standard library function ready exists to test whether a timer has expired. See Timer functions for details.
Channel expressions
Channels are used to connect processes with each other. See the Channel type for details.
Usually, channels are created by variable declarations, as in:
chan void s;
chan int c, d;This creates three channels, one synchronization channel s, and two channels (c, and d) communicating integers.
There is also a channel function to make new channels:
-
chan Tchannel(T) -
Construct a new channel communicating data type
T. WhenTisvoid, a synchronization channel is created instead.
The only binary expressions on channels are equality comparison operations.
| Expression | Type lhs | Type rhs | Type result | Explanation |
|---|---|---|---|---|
|
lhs |
chan T |
chan T |
bool |
Test for equality |
|
lhs |
chan T |
chan T |
bool |
Test for inequality |
where T can be either a normal type, or void. There has to be an overlap between the channel directions (that is, you cannot compare a receive-only channel with a send-only channel).
Distribution expressions
A distribution represents a stochastic distribution for drawing random numbers. It use a pseudo-random number generator. See Modeling stochastic behavior for a discussion how random numbers are used.
Variables of type distribution (see Distribution type) are initialized by using a distribution function from the standard library, see Distributions for an overview.
There is only one operator for variables with a distribution type, as shown below.
| Expression | Type op | Type result | Explanation |
|---|---|---|---|
|
|
dist bool |
bool |
Sample op distribution |
|
|
dist int |
int |
Sample op distribution |
|
|
dist real |
real |
Sample op distribution |
The sample operator draws a random number from a distribution. For example rolling a dice:
model Dice():
dist int d = uniform(1, 7);
# Roll the dice 5 times
for i in range(5):
writeln("Rolled %d", sample d);
end
endProcess expressions
A process expression refers to a process definition. It can be used to parameterize the process that is being instantiated, by passing such a value to a run or start statement. (See Run and start statements for details on how to create a new process.) An example:
proc A(int x):
writeln("A(%d)", x);
end
proc B(int x):
writeln("B(%d)", x);
end
proc P(proc (int) ab):
run ab(3);
end
model M():
run P(A); # Pass 'proc A' into P.
endFormal parameter ab of process P is a process variable that refers to a process taking an integer parameter. The given process definition is instantiated. Since in the model definition, A is given to process P, the output of the above model is A(3).
Instance expressions
Process instances represent running processes in the model. Their use is to store a reference to such a running process, to allow testing for finishing.
An instance variable is assigned during a start statement. (See Run and start statements for details on how to start a new process.)
The instance variable is used to test for termination of the instantiated process, or to wait for it:
proc Wait():
delay 4.52;
end
model M():
inst w;
start w = Wait();
delay 1.2;
writeln("is Wait finished? %b", finished(w));
# Wait until the process has finished.
finish w;
endWait is a process that waits a while before terminating. In the start statement, instance variable w is set up to refer to instantiated process Wait. After assignment, you can use the variable for testing whether the process has terminated. In the example, the test result is written to the screen, but this could also be used as a guard in a select statement (See Select statement for details).
The other thing that you can do is to wait for termination of the process by means of the finish statement, see also Finish statement.
Matrix expression
The syntax of a matrix literal value is as follows.
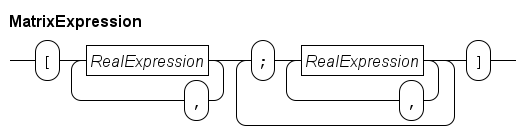
The literal starts with a [ symbol, and ends with a ] symbol. In between it has at least two comma-separated lists of real number values, separated with a ; symbol.
Each comma-separated list of real number values is a row of the matrix. The number of columns of each row is the same at each row, which means the number of real number values must be the same with each list. As an example:
matrix(2, 3) m = [1.0, 2.0, 3.0;
4.0, 5.0, 6.0]m is a matrix with two rows and three columns. A comma separates two columns from each other, a semicolon separates two rows.
The syntax demands at least one semicolon in a literal matrix value, which means you cannot write a matrix literal with a single row directly. Instead, write a cast expression that converts a list of real numbers to a matrix with a single row. See Cast expressions for an explanation of cast expressions.
Cast expressions
A cast expression converts a value from one type to another. The syntax of a cast expression is as follows.
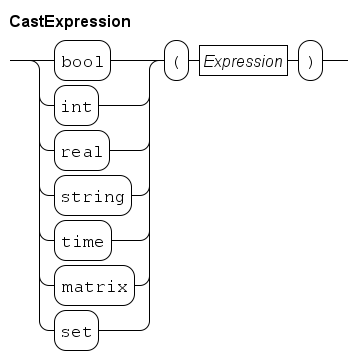
You write the result type, followed by an expression between parentheses. The value of the expression is converted to the given type. For example:
real v = 3.81;
timer t;
t = timer(v); # Convert from real to timer (third entry in the table)The conversion from a list to a matrix (the first entry in the table) is a special case in the sense that you also need to specify the size of the resulting matrix, as in:
list real xs = [1, 2, 3];
writeln("matrix with one row and three columns: %s", matrix(1, 3, xs));The expected number of rows and columns given in the first two arguments must be constant. When the conversion is performed, the length of the given list must be the same as the number of columns stated in the second argument.
The number of available conversions is quite limited, below is a table that lists them.
| Value type | Result type | Remarks |
|---|---|---|
|
list |
matrix |
Conversion of a list to a matrix with one row |
|
list |
set |
Construct a set from a list |
|
real |
timer |
Setting up a timer |
|
timer |
real |
Reading the current value of a timer |
|
string |
bool |
Parsing a boolean value from a string |
|
string |
int |
Parsing an integer number from a string |
|
string |
real |
Parsing a real number from a string |
|
bool |
string |
Converting a boolean to a string representation |
|
int |
string |
Converting an integer to a string representation |
|
real |
string |
Converting a real number to a string representation |
|
int |
real |
Widening an integer number to a real number |
The first entry exists for creating matrices with one row (which you cannot write syntactically). The second entry constructs a set from a list of values. The element type of the list and the resulting set are the same.
The pair of conversions between timer type and real number type is for setting and reading timers, see Timers for their use.
The conversions from string to boolean or numeric allows parsing of a string. The other way around is also possible, although this is usually done as part of a write statement (see Write statement for details).
The final entry is for widening an integer to a real number. The other way around (from a real number to an integer number) does not exist as cast, but there are stdlib functions ceil, floor, and round available instead (explained in Real number functions).
Function call expressions
A function call starts a function to compute its result value from the input parameters. The syntax is as follows.
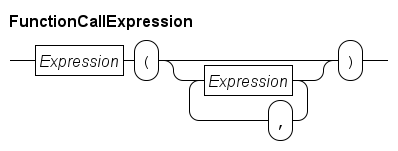
The Expression before the open parenthesis represents the function to call. Often this is a simple name like size (the name of one of the standard library functions), but you can have more complicated expressions.
The sequence of expressions inside the parentheses denote the values of the input parameters of the functions. Their type has to match with the type stated in the formal parameter at the corresponding position.
The result of the function call is a value with the same type as stated in the return type of the function definition.
Operator priorities
Operator priorities aim to reduce the number of parentheses needed in expressions. They do this by make choices in the order of applying operators on their arguments. For example, 1 + 2 * 3 can be interpreted as (1 + 2) * 3 (if the addition operation is applied first), or as 1 + (2 * 3) (if the multiplication operation is performed first).
In the following table, the order of applying operators in the Chi language is defined.
| Priority | Operators |
|---|---|
|
1 |
(unary) |
|
2 |
unary |
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
(unary) |
|
8 |
|
|
9 |
|
Operators with a smaller priority number get applied before operators with a higher priority number. Operators with the same priority get applied from left to right.