Channels

> >

In Processes processes have been introduced. This chapter describes channels, denoted by the type chan. A channel connects two processes and is used for the transfer of data or just signals. One process is the sending process, the other process is the receiving process. Communication between the processes takes place instantly when both processes are willing to communicate, this is called synchronous communication.

A channel

The following example shows the sending of an integer value between two processes via a channel. The figure below shows the two processes P and C, connected by channel variable a:

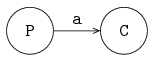
Processes are denoted by circles, and channels are denoted by directed arrows in the figure. The arrow denotes the direction of communication. Process P is the sender or producer, process C is the receiver or consumer.

In this case, the producer sends a finite stream of integer values (5 numbers) to the consumer. The consumer receives these values and writes them to the screen. The model is:

proc P(chan! int a):
    for i in range(5):
        a!i
    end
end

proc C(chan? int b):
    int x;

    while true:
        b?x;
        write("%d\n",x)
    end
end

model M():
    chan int a;

    run P(a), C(a)
end

The model instantiates processes P and C. The two processes are connected to each other via channel variable a which is given as actual parameter in the run statement. This value is copied into the local formal parameter a in process P and in formal parameter b inside process C.

Process P can send a value of type int via the actual channel parameter a to process C. In this case P first tries to send the value 0. Process C tries to receive a value of type int via the actual channel parameter a. Both processes can communicate, so the communication occurs and the value 0 is sent to process C. The received value is assigned in process C to variable x. The value of x is printed and the cycle starts again. This model writes the sequence 0, 1, 2, 3, 4 to the screen.

Synchronization channels

Above, process P constructs the numbers and sends them to process C. However, since it is known that the number sequence starts at 0 and increments by one each time, there is no actual need to transfer a number. Process C could also construct the number by itself after getting a signal (a 'go ahead') from process P. Such signals are called synchronization signals, transfered by means of a synchronization channel. The signal does not carry any data, it just synchronizes a send and a receive between different processes. (Since there is no actual data transfered, the notion of sender and receiver is ambiguous. However, in modeling there is often a notion of 'initiator' process that can be conveniently expressed with sending.)

The following example shows the use of synchronization signals between processes P and C. The connecting channel 'transfers' values of type void. The type void means that 'non-values' are sent and received; the type void is only allowed in combination with channels. The iconic model is given in the previous figure, at the start of this chapter. The model is:

proc P(chan! void a):
    for i in range(5):
        a!    # No data is being sent
    end
end

proc C(chan? void b):
    int i;

    while true:
        b?;   # Nothing is being received
        write("%d\n", i);
        i = i + 1
    end
end

model M():
    chan void a;

    run P(a), C(a)
end

Process P sends a signal (and no value is sent), and process C receives a signal (without a value). The signal is used by process C to write the value of i and to increment variable i. The effect of the model is identical to the previous example: the numbers 0, 1, 2, 3, 4 appear on the screen.

Two channels

A process can have more than one channel, allowing interaction with several other processes.

The next example shows two channel variables, a and b, and three processes, generator G, server S and exit E. The iconic model is given below:

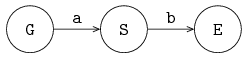
Process G is connected via channel variable a to process S and process S is connected via channel variable b to process E. The model is:

proc G(chan! int a):
    for x in range(5):
        a!x
    end
end

proc S(chan? int a; chan! int b):
    int x;

    while true:
        a?x; x = 2 * x; b!x
    end
end

proc E(chan int a):
    int x;

    while true:
        a?x;
        write("E %d\n", x)
    end
end

model M():
    chan int a,b;

    run G(a), S(a,b), E(b)
end

The model contains two channel variables a and b. The processes are connected to each other in model M. The processes are instantiated and run where the formal parameters are replaced by the actual parameters. Process G sends a stream of integer values 0, 1, 2, 3, 4 to another process via channel a. Process S receives a value via channel a, assigns this value to variable x, doubles the value of the variable, and sends the value of the variable via b to another process. Process E receives a value via channel b, assigns this value to the variable x, and prints this value. The result of the model is given by:

After printing this five lines, process G stops, process S is blocked, as well as process E, the model gets blocked, and the model ends.

More senders or receivers

Channels send a message (or a signal in case of synchronization channels) from one sender to one receiver. It is however allowed to give the same channel to several sender or receiver processes. The channel selects a sender and a receiver before each communication.

The following example gives an illustration:

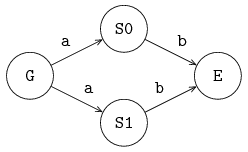
Suppose that only G and S0 want to communicate. The channel can select a sender (namely G) and a receiver (process S0), and let both processes communicate with each other. When sender G, and both receivers (S0 and S1), want to communicate, the channel selects a sender (G as it is the only sender available to the channel), and a receiver (either process S0 or process S1), and it lets the selected processes communicate with each other. This selection process is non-deterministic; a choice is made, but it is unknown how the selection takes place and it cannot be influenced. Note that a non-deterministic choice is different from a random choice. In the latter case, there are known probabilities of selecting a process.

Sharing a channel in this way allows to send data to receiving processes where the receiving party is not relevant (either server process will do). This way of communication is different from broadcasting, where both servers receive the same data value. Broadcasting is not supported by the Chi language.

In case of two senders, S0 and S1, and one receiver E the selection process is the same. If one of the two servers S can communicate with exit E, communication between that server and the exit takes place. If both servers can communicate, a non-deterministic choice is made.

Having several senders and several receivers for a single channel is also handled in the same manner. A non-deterministic choice is made for the sending process and a non-deterministic choice is made for the receiving process before each communication.

To communicate with several other processes but without non-determinism, unique channels must be used.

Notes

The direction in channels, denoted by ? or !, may be omitted. By leaving it out, the semantics of the parameters becomes less clear (the direction of communication has to be derived from the process code).
There are a several ways to name channels:
1. Start naming formal channel parameters in each new process with a, b, etc. The actual names follow from the figure. This convention is followed in this chapter. For small models this convention is easy and works well, for complicated models this convention can be error-prone.
2. Use the actual names of the channel parameters in the figures as formal names in the processes. Start naming in figures with a, b, etc. This convention works well, if both figure and code are at hand during the design process. If many processes have sub-processes, this convention does not really work.
3. Use unique names for the channel parameters for the whole model, and for all sub-systems, for example a channel between processes A and B is named a2b (the lower-case name of the sending process, followed by 2, denoting 'to', and the lower-case name of the receiving process).
  
  In this case the formal and actual parameters can be in most cases the same. If many identical processes are used, this convention does not really work.

In the text all three conventions are used, depending on the structure of the model.

Exercises

Given is the specification of process P and model PP:

proc P(chan int a, b):
    int x;

    while true:
        a?x;
        x = x + 1;
        write("%d\n", x);
        b!x
    end
end

model PP():
    chan int a, b;

    run P(a,b), P(b,a)
end

Study this specification.
Why does the model terminate immediately?

Six children have been given the assignment to perform a series of calculations on the numbers 0, 1, 2, 3, ..., 9, namely add 2, multiply by 3, multiply by 2, and add 6 subsequently. They decide to split up the calculations and to operate in parallel. They sit down at a table next to each other. The first child, the reader R, reads the numbers 0, 1, 2, 3, ..., 9 one by one to the first calculating child C1. Child C1 adds 2 and tells the result to its right neighbour, child C2. After telling the result to child C2, child C1 is able to start calculating on the next number the reader R tells him. Children C2, C3, and C4 are analogous to child C1; they each perform a different calculation on a number they hear and tell the result to their right neighbor. At the end of the table the writer W writes every result he hears down on paper. A schematic drawing of the children at the table, is given below: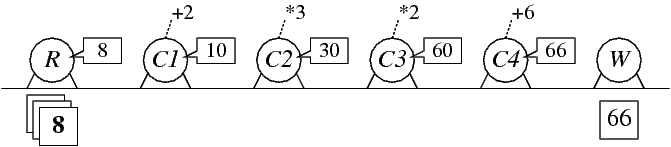
1. Finish the specification for the reading child R, that reads the numbers 0 till 9 one by one:
  proc R(...): int i; while i < 10: ...; ... end end
2. Specify the parameterized process Cadd that represents the children C1 and C4, who perform an addition.
3. Specify the parameterized process Cmul that represents the children C2 and C3, who perform a multiplication.
4. Specify the process W representing the writing child. Write each result to the screen separated by a new line.
5. Make a graphical representation of the model SixChildren that is composed of the six children.
6. Specify the model SixChildren. Simulate the model.