Data types
The language is a statically typed language, which means that all variables and values in a model have a single fixed type. All variables must be declared in the program. The declaration of a variable consists of the type, and the name, of the variable. The following fragment shows the declaration of two elementary data types, integer variable i and real variable r:
...
int i;
real r;
...The ellipsis (...) denotes that non-relevant information is left out from the fragment. The syntax for the declaration of variables is similar to the language C. All declared variables are initialized, variables i and r are both initialized to zero.
An expression, consisting of operators, e.g. plus (+), times (*), and operands, e.g. i and r, is used to calculate a new value. The new value can be assigned to a variable by using an assignment statement. An example with four variables, two expressions and assignment statements is:
...
int i = 2, j;
real r = 1.50, s;
j = 2 * i + 1;
s = r / 2;
...The value of variable j becomes 5, and the value of s becomes 0.75. Statements are described in Statements.
Data types are categorized in five different groups: elementary types, tuple types, container types, custom types, and distribution types. Elementary types are types such as Boolean, integer, real or string. Tuple types contain at least one element, where each element can be of different type. In other languages tuple types are called records (Pascal) or structures (C). Variables with a container type (a list, set, or dictionary) contain many elements, where each element is of the same type. Custom types are created by the user to enhance the readability of the model. Distributions types are types used for the generation of distributions from (pseudo-) random numbers. They are covered in Modeling stochastic behavior.
Elementary types
The elementary data types are Booleans, numbers and strings. The language provides the elementary data types:
-
boolfor booleans, with valuesfalseandtrue. -
enumfor enumeration types, for exampleenum FlagColors = {red, white, blue}, -
intfor integers, e.g.-7,20,0. -
realfor reals, e.g.3.14,7.0e9. -
stringfor text strings, e.g."Hello","world".
Booleans
A boolean value has two possible values, the truth values. These truth values are false and true. The value false means that a property is not fulfilled. A value true means the presence of a property. Boolean variables are initialized with the value false.
In mathematics, various symbols are used for unary and binary boolean operators. These operators are also present in Chi. The most commonly used boolean operators are not, and, and or. The names of the operators, the symbols in mathematics and the symbols in the language are presented in the following table:
| Operator | Math | Chi |
|---|---|---|
|
boolean not |
¬ |
|
|
boolean and |
∧ |
|
|
boolean or |
∨ |
|
Examples of boolean expressions are the following. If z equals true, then the value of (not z) equals false. If s equals false, and t equals true, then the value of the expression (s or t) becomes true.
The result of the unary not, the binary and and or operators, for two variables p and q is given in the following table:
p |
q |
not p |
p and q |
p or q |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
If p = true and q = false, we find for p or q the value true (third line in the table).
Enumerations
Often there are several variants of entities, like types of products, available resources, available machine types, and so on.
One way of coding them is give each a unique number, which results in code with a lot of small numbers that are not actually numbers, but refer to one variant.
Another way is to give each variant a name (which often already exists), and use those names instead.
For example, to model a traffic light:
enum TrafficColor = {RED, ORANGE, GREEN};
TrafficColor light = RED;The enum TrafficColor line lists the available traffic colors. With this definition, a new type TrafficColor is created, which you can use like any other type. The line TrafficColor light = RED; creates a new variable called light and initializes it to the value RED.
Numbers
In the language, two types of numbers are available: integer numbers and real numbers. Integer numbers are whole numbers, denoted by type int e.g. 3, -10, 0. Real numbers are used to present numbers with a fraction, denoted by type real. E.g. 3.14, 2.7e6 (the scientific notation for 2.7 million). Note that real numbers must either have a fraction or use the scientific notation, to let the computer know you mean a real number (instead of an integer number). Integer variables are initialized with 0. Real variables are initialized with 0.0.
For numbers, the normal arithmetic operators are defined. Expressions can be constructed with these operators. The arithmetic operators for numbers are listed in the following table:
| Operator name | Notation | Comment |
|---|---|---|
|
unary plus |
|
|
|
unary minus |
|
|
|
raising to the power |
|
Always a |
|
multiplication |
|
|
|
real division |
|
Always a |
|
division |
|
For |
|
modulo |
|
For |
|
addition |
|
|
|
subtraction |
|
The priority of the operators is given from high to low. The unary operators have the strongest binding, and the + and - the weakest binding. So, -3^2 is read as (-3)^2 and not -(3^2), because the priority rules say that the unary operator binds stronger than the raising to the power operator. Binding in expressions can be changed by the use of parentheses.
The integer division, denoted by div, gives the biggest integral number smaller or equal to x / y. The integer remainder, denoted by mod, gives the remainder after division x - y * (x div y). So, 7 div 3 gives 2 and -7 div 3 gives -3, 7 mod 3 gives 1 and -7 mod 3 gives 2.
The rule for the result of an operation is as follows. The real division and raising to the power operations always produce a value of type real. Otherwise, if both operands (thus x and y) are of type int, the result of the operation is of type int. If one of the operands is of type real, the result of the operation is of type real.
Conversion functions exist to convert a real into an integer. The function ceil converts a real to the smallest integer value not less than the real, the function floor gives the biggest integer value smaller than or equal to the real, and the function round rounds the real to the nearest integer value (or up, if it ends on .5).
Between two numbers a relational operation can be defined. If for example variable x is smaller than variable y, the expression x < y equals true. The relational operators, with well-known semantics, are listed in the following table:
| Name | Operator |
|---|---|
|
less than |
|
|
at most |
|
|
equals |
|
|
differs from |
|
|
at least |
|
|
greater than |
|
Strings
Variables of type string contains a sequence of characters. A string is enclosed by double quotes. An example is "Manufacturing line". Strings can be composed from different strings. The concatenation operator (+) adds one string to another, for example "One" + " " + "string" gives "One string". Moreover the relational operators (<, <=, ==, != >=, and >) can be used to compare strings alphabetically, e.g. "a" < "aa" < "ab" < "b". String variables are initialized with the empty string "".
Tuple types
Tuple types are used for keeping several (related) kinds of data together in one variable, e.g. the name and the age of a person. A tuple variable consists of a number of fields inside the tuple, where the types of these fields may be different. The number of fields is fixed. One operator, the projection operator denoted by a dot (.), is defined for tuples. It selects a field in the tuple for reading or assigning.
Notation
A type person is a tuple with two fields, a 'name' field of type string, and an 'age' field of type int, is denoted by:
type person = tuple(string name; int age)Operator
A projection operator fetches a field from a tuple. We define two persons:
person eva = ("eva" , 29),
adam = ("adam", 27);And we can speak of eva.name and adam.age, denoting the name of eva ("eva") and the age of adam (27). We can assign a field in a tuple to another variable:
ae = eva.age;
eva.age = eva.age + 1;This means that the age of eva is assigned tot variable ae, and the new age of eva becomes eva.age + 1.
By using a multi assignment statement all values of a tuple can be copied into separate variables:
string name;
int age;
name, age = evaThis assignment copies the name of eva into variable name of type string and her age into age of type int.
Container types
Lists, sets and dictionaries are container types. A variable of this type contains zero or more identical elements. Elements can be added or removed in variables of these types. Variables of a container type are initialized with zero elements.
Sets are unordered collections of elements. Each element value either exists in a set, or it does not exist in a set. Each element value is unique, duplicate elements are silently discarded. A list is an ordered collection of elements, that is, there is a first and a last element (in a non-empty list). A list also allows duplicate element values. Dictionaries are unordered and have no duplicate value, just like sets, but you can associate a value (of a different type) with each element value.
Lists are denoted by a pair of (square) brackets. For example, [7, 8, 3] is a list with three integer elements. Since a list is ordered, [8, 7, 3] is a different list. With empty lists, the computer has to know the type of the elements, e.g. <int>[] is an empty list with integer elements. The prefix <int> is required in this case.
Sets are denoted by a pair of (curly) braces, e.g. {7, 8, 3} is a set with three integer elements. As with lists, for an empty set a prefix is required, for example <string>{} is an empty set with strings. A set is an unordered collection of elements. The set {7, 8, 3} is a set with three integer numbers. Since order of the elements does not matter, the same set can also be written as {8, 3, 7} (or in one of the four other orders). In addition, each element in a set is unique, the set {8, 7, 8, 3} is equal to the set {7, 8, 3}. For readability, elements in a set are normally written in increasing order, for example {3, 7, 8}.
Dictionaries are denoted by a pair of (curly) braces, whereby an element value consists of two parts, a 'key' and a 'value' part. The two parts separated by a colon (:). For example {"jim" : 32, "john" : 34} is a dictionary with two elements. The first element has "jim" as key part and 32 as value part, the second element has "john" as key part and 34 as value part. The key parts of the elements work like a set, they are unordered and duplicates are silently discarded. A value part is associated with its key part. In this example, the key part is the name of a person, while the value part keeps the age of that person. Empty dictionaries are written with a type prefix just like lists and sets, e.g. <string:int>{}.
Container types have some built-in functions in common (Functions are described in Functions):
-
The function
sizegives the number of elements in a variable, for examplesize([7, 8, 3])yields 3;size({7, 8})results in 2;size({"jim":32})gives 1 (an element consists of two parts).
-
The function
emptyyieldstrueif there are no elements in variable. E.g.empty(<string>{})with an empty set of typestringis true. (Here the typestringis needed to determine the type of the elements of the empty set.)
-
The function
popextracts a value from the provided collection and returns a tuple with that value, and the collection minus the value.For lists, the first element of the list becomes the first field of the tuple. The second field of the tuple becomes the list minus the first list element. For example:
pop([7, 8, 3]) -> (7, [8, 3])The
->above denotes 'yields'. The value of the list is split into a 'head' (the first element) and a 'tail' (the remaining elements).For sets, the first field of the tuple becomes the value of an arbitrary element from the set. The second field of the tuple becomes the original set minus the arbitrary element. For example, a
popon the set{8, 7, 3}has three possible answers:pop({8, 7, 3}) -> (7, {3, 8}) or pop({8, 7, 3}) -> (3, {7, 8}) or pop({8, 7, 3}) -> (8, {3, 7})Performing a
popon a dictionary follows the same pattern as above, except 'a value from the collection' are actually a key item and a value item. In this case, thepopfunction gives a three-tuple as result. The first field of the tuple becomes the key of the extracted element, the second field of the tuple becomes the value of the element, and the third field of the tuple contains the dictionary except for the extracted element. Examples:pop({"a" : 32, "b" : 34}) -> ("a", 32, {"b" : 34}) or pop({"a" : 32, "b" : 34}) -> ("b", 34, {"a" : 32})
Lists
A list is an ordered collection of elements of the same type. They are useful to model anything where duplicate values may occur or where order of the values is significant. Examples are waiting customers in a shop, process steps in a recipe, or products stored in a warehouse. Various operations are defined for lists.
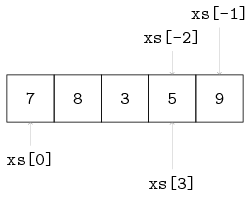
An element can be fetched by indexing. This indexing operation does not change the content of the variable. The first element of a list has index 0. The last element of a list has index size(xs) - 1. A negative index, say m, starts from the back of the list, or equivalently, at offset size(xs) + m from the front. You cannot index non-existing elements. Some examples, with xs = [7, 8, 3, 5, 9] are:
xs[0] -> 7
xs[3] -> 5
xs[5] -> ERROR (there is no element at position 5)
xs[-1] -> xs[5 - 1] -> xs[4] -> 9
xs[-2] -> xs[5 - 2] -> xs[3] -> 5In the figure below, the list with indices is visualized. A common name for the first element of a list (i.e., x[0]) is the head of a list. Similarly, the last element of a list (xs[-1]) is also known as head right.
A part of a list can be fetched by slicing. The slicing operation does not change the content of the list, it copies a contiguous sequence of a list. The result of a slice operation is again a list, even if the slice contains just one element.
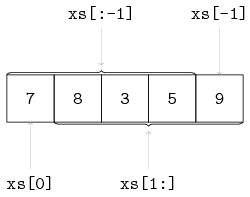
Slicing is denoted by xs[i:j]. The slice of xs[i:j] is defined as the sequence of elements with index k such that i <= k < j. Note the upper bound j is noninclusive. If i is omitted use 0. If j is omitted use size(xs). If i is greater than or equal to j, the slice is empty. If i or j is negative, the index is relative to the end of the list: size(xs) + i or size(xs) + j is substituted. Some examples with xs = [7, 8, 3, 5, 9]:
xs[1:3] -> [8, 3]
xs[:2] -> [7, 8]
xs[1:] -> [8, 3, 5, 9]
xs[:-1] -> [7, 8, 3, 5]
xs[:-3] -> [7, 8]The list of all but the first elements (xs[1:]) is often called tail and xs[:-1] is also known as tail right. Below, the slicing operator is visualized:
Two lists can be 'glued' together into a new list. The glue-ing or concatenation of a list with elements 7, 8, 3 and a list with elements 5, and 9 is denoted by:
[7, 8, 3] + [5, 9] -> [7, 8, 3, 5, 9]An element can be added to a list at the rear or at the front. The action is performed by transforming the element into a list and then concatenate these two lists. In the next example the value 5 is added to the rear, respectively the front, of a list:
[7, 8, 3] + [5] -> [7, 8, 3, 5]
[5] + [7, 8, 3] -> [5, 7, 8, 3]Elements also can be removed from a list. The del function removes by position, e.g. del(xs, 2) returns the list xs without its third element (since positions start at index 0). Removing a value by value can be performed by the subtraction operator -. For instance, consider the following subtractions:
[1, 4, 2, 4, 5] - [2] -> [1, 4, 4, 5]
[1, 4, 2, 4, 5] - [4] -> [1, 2, 4, 5]
[1, 4, 2, 4, 5] - [8] -> [1, 4, 2, 4, 5]Every element in the list at the right is searched in the list at the left, and if found, the first occurrence is removed. In the first example, element 2 is removed. In the second example, only the first value 4 is removed and the second value (at position 3) is kept. In the third example, nothing is removed, since value 8 is not in the list at the left.
When the list at the right is longer than one element, the operation is repeated. For example, consider xs - ys, whereby xs = [1, 2, 3, 4, 5] and ys = [6, 4, 2, 3]. The result is computed as follows:
[1, 2, 3, 4, 5] - [6, 4, 2, 3]
-> ([1, 2, 3, 4, 5] - [6]) - [4, 2, 3]
-> [1, 2, 3, 4, 5] - [4, 2, 3]
-> ([1, 2, 3, 4, 5] - [4]) - [2, 3]
-> [1, 2, 3, 5] - [2, 3]
-> ([1, 2, 3, 5] - [2]) - [3]
-> [1, 3, 5] - [3]
-> [1,5]Lists have two relational operators, the equal operator and the not-equal operator. The equal operator (==) compares two lists. If the lists have the same number of elements and all the elements are pair-wise the same, the result of the operation is true, otherwise false. The not-equal operator (!=) does the same check, but with an opposite result. Some examples, with xs = [7, 8, 3]:
xs == [7, 8, 3] -> true
xs == [7, 7, 7] -> falseThe membership operator (in) checks if an element is in a list. Some examples, with xs = [7, 8, 3]:
6 in xs -> false
7 in xs -> true
8 in xs -> trueInitialization
A list variable is initialized with a list with zero elements, for example in:
list int xs;The initial value of xs equals <int>[].
A list can be initialized with a number, denoting the number of elements in the list:
list(2) int ysThis declaration creates a list with 2 elements, whereby each element of type int is initialized. The initial value of ys equals [0, 0]. Another example with a list of lists:
list(4) list(2) int zmThis declaration initializes variable zm with the value [ [0, 0], [0, 0], [0, 0], [0, 0] ].
Sets
Set operators for union, intersection and difference are present. The table below gives the name, the mathematical notation and the notation in the Chi language:
| Operator | Math | Chi |
|---|---|---|
|
set union |
∪ |
|
|
set intersection |
∩ |
|
|
set difference |
∖ |
|
The union of two sets merges the values of both sets into one, that is, the result is the collection of values that appear in at least one of the arguments of the union operation. Some examples:
{3, 7, 8} + {5, 9} -> {3, 5, 7, 8, 9}All permutations with the elements 3, 5, 7, 8 and 9 are correct (sets have no order, all permutations are equivalent). To keep sets readable the elements are sorted in increasing order in this tutorial.
Values that occur in both arguments, appear only one time in the result (sets silently discard duplicate elements). For example:
{3, 7, 8} + {7, 9} -> {3, 7, 8, 9}The intersection of two sets gives a set with the common elements, that is, all values that occur in both arguments. Some examples:
{3, 7, 8} * {5, 9} -> <int>{} # no common element
{3, 7, 8} * {7, 9} -> {7} # only 7 in commonSet difference works much like subtraction on lists, except elements occur at most one time (and have no order). The operation computes 'remaining elements'. The result is a new set containing all values from the first set which are not in the second set. Some examples:
{3, 7, 8} - {5, 9} -> {3, 7, 8}
{3, 7, 8} - {7, 9} -> {3, 9}The membership operator in works on sets too:
3 in {3, 7, 8} -> true
9 in {3, 7, 8} -> falseDictionaries
Elements of dictionaries are stored according to a key, while lists elements are ordered by a (relative) position, and set elements are not ordered at all. A dictionary can grow and shrink by adding or removing elements respectively, like a list or a set. An element of a dictionary is accessed by the key of the element.
The dictionary variable d of type dict(string : int) is given by:
dict (string : int) d =
{"jim" : 32,
"john" : 34,
"adam" : 25}Retrieving values of the dictionary by using the key:
d["john"] -> 34
d["adam"] -> 25Using a non-existing key to retrieve a value results in a error message.
A new value can be assigned to the variable by selecting the key of the element:
d["john"] = 35This assignment changes the value of the "john" item to 35. The assignment can also be used to add new items:
d["lisa"] = 19Membership testing of keys in dictionaries can be done with the in operator:
"jim" in d -> true
"peter" in d -> falseMerging two dictionaries is done by adding them together. The value of the second dictionary is used when a key exists in both dictionaries:
{1 : 1, 2 : 2} + {1 : 5, 3 : 3} -> {1 : 5, 2 : 2, 3 : 3}The left dictionary is copied, and updated with each item of the right dictionary.
Removing elements can be done with subtraction, based on key values. Lists and sets can also be used to denote which keys should be removed. A few examples for p is {1 : 1, 2 : 2}:
p - {1 : 3, 5 : 5} -> {2 : 2}
p - {1, 7} -> {2 : 2}
p - [2, 8] -> {1 : 1}Subtracting keys that do not exist in the left dictionary is allowed and has no effect.
Custom types
To structure data the language allows the creation of new types. The definition can only be done at global level, that is, outside any proc, func, model, or xper definition.
Types can be used as alias for elementary data types to increase readability, for example a variable of type item:
type item = real;Variables of type item are, e.g.:
item box, product;
box = 4.0; product = 120.5;This definition creates the possibility to speak about an item.
Types also can be used to make combinations of other data types, e.g. a recipe:
type step = tuple(string name; real process_time),
recipe = tuple(int id; list step steps);A type step is defined by a tuple with two fields, a field with name of type string, denoting the name of the step, and a field with process_time of type real, denoting the duration of the (processing) step. The step definition is used in the type recipe. Type recipe is defined by a tuple with two fields, an id of type int, denoting the identification number, and a field steps of type list step, denoting a list of single steps. Variables of type recipe are, e.g.:
recipe plate, bread;
plate = (34, [("s", 10.8), ("w", 13.7), ("s", 25.6)]);
bread = (90, [("flour", 16.3), ("yeast", 6.9)]);Exercises
-
Exercises for integer numbers. What is the result of the following expressions:
-5 ^ 3 -5 * 3 5 mod 3 -
Exercises for tuples. Given are tuple type
boxand variablexof typebox:type box = tuple(string name; real weight); box x = ("White", 12.5);What is the result of the following expressions:
x.name x.real x -
Exercises for lists. Given is the list
xs = [0,1,2,3,4,5,6]. Determine the outcome of:xs[0] xs[1:] size(xs) xs + [3] [4,5] + xs xs - [2,2,3] xs - xs[2:] xs[0] + (xs[1:])[0]