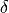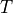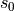Driver

AlgorithmAgentFollowingDriverModel

AlgorithmAgentFollowingDriverModel implements a simple driver model for longitudinal and lateral control.

Lateral control

The lateral guidance always keeps the agent in the middle of the lane.

Longitudinal control

This driver type works according to the IDM (Intelligent Driver Model) and adapts its velocity to an agent in front and holds a desired velocity if there’s no front agent available (like adaptive cruise control).

For a simplified version of the model, the Intelligent Driver Model acceleration 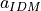$a_{IDM}$ is described by the following equation:

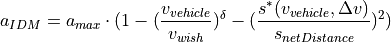
$a_{IDM} = a_{max} \cdot (1 - (\frac{v_{vehicle}}{v_{wish}})^\delta - (\frac{s^*(v_{vehicle},\Delta v)}{s_{netDistance}})^2)$

with

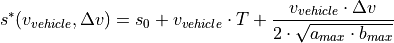
$s^*(v_{vehicle},\Delta v) = s_{0} + v_{vehicle} \cdot T + \frac{v_{vehicle} \cdot \Delta v}{2 \cdot \sqrt{a_{max} \cdot b_{max}}}$

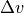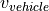The calculation of $\Delta v$ is done by subtracting the absolute velocity $v_{vehicle}$ of the own vehicle from the absolute velocity $v_{frontAgent}$ of the front agent:

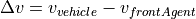
$\Delta v = v_{vehicle} - v_{frontAgent}$

The acceleration of the vehicle (Intelligent Driver Model acceleration) can be separated into

free road term:

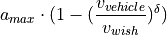
$a_{max} \cdot (1 - (\frac{v_{vehicle}}{v_{wish}})^\delta)$

interaction term:

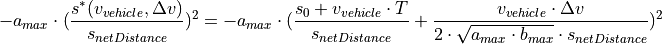
$-a_{max} \cdot (\frac{s^*(v_{vehicle},\Delta v)}{s_{netDistance}})^2 = -a_{max} \cdot (\frac{s_{0} + v_{vehicle} \cdot T}{s_{netDistance}} + \frac{v_{vehicle} \cdot \Delta v}{2 \cdot \sqrt{a_{max} \cdot b_{max}} \cdot s_{netDistance}})^2$

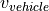Free road behavior: On a free road, the distance to the front agent is huge and the vehicle’s acceleration is controlled by the free road term, which is approximately equal to $a_{max}$ for low velocities and vanishes as $v_{vehicle}$ approaches 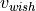$v_{wish}$ . There will be some deviation to the actual vehicle velocity, due to the model not being aware of air drag or engine drag (which might be introduced by subsequent agent components). AlgorithmAgentFollowingDriverModel just controls its velocity wish.

Behavior at high approaching rates: For large velocity differences, the interaction term is governed by:

$-a_{max} \cdot (\frac{v_{vehicle} \cdot \Delta v}{2 \cdot \sqrt{a_{max} \cdot b_{max}} \cdot s_{netDistance}})^2$

This leads to a driving behavior that compensates velocity differences while trying not to brake much harder than the maximum braking deceleration $b_{max}$ .

Behavior at small net distances: For minor velocity differences and small net distances, the interaction term is approximately equal to:

$-a_{max} \cdot (\frac{s_{0} + v_{vehicle} \cdot T}{s_{netDistance}})^2$

which resembles a simple repulsive force such that small net distances are quickly enlarged towards an equilibrium net distance.

The following table and the DriverProfile snippet describe a whole DriverProfile. Type “AlgorithmAgentFollowingDriverModel” in the DriverProfile snippet below determines that this set of parameters is active.

Parameter	Type	Unit	Description	Defaults to
AlgorithmLateralModule	String		Behavior model for the steering wheel angle of the driver	Required value
AlgorithmLongitudinalModule	String		Behavior model for the accelerator, brake pedal position, and the current gear of the driver	Required value
VelocityWish: $v_{wish}$	Double	m/s	Desired speed	33.33 m/s
Delta: $\delta$	Double		Free acceleration exponent characterizing how the acceleration decreases with velocity (1: linear, infinity: constant)	4.0
TGapWish: $T$	Double	s	Desired time gap between ego and front agent	1.5 s
MinDistance: $s_{0}$	Double	m	Minimum distance between ego and front (used at slow speeds); Also called jam distance	2.0 m
MaxAcceleration: $a_{max}$	Double	m/s²	Maximum acceleration in satisfactory way, not vehicle possible acceleration	1.4 m/s²
MaxDeceleration: $b_{max}$	Double	m/s²	Desired deceleration	2.0 m/s²

<Profile Name="Regular">
  <String Key="Type" Value="AlgorithmAgentFollowingDriverModel"/>
  <String Key="AlgorithmLateralModule" Value="Algorithm_LateralAfdm"/>
  <String Key="AlgorithmLongitudinalModule" Value="Algorithm_LongitudinalAfdm"/>
  <Double Key="VelocityWish" Value="36.11"/>
  <Double Key="Delta" Value="4.0"/>
  <Double Key="TGapWish" Value="1.5"/>
  <Double Key="MinDistance" Value="2.0"/>
  <Double Key="MaxAcceleration" Value="1.4"/>
  <Double Key="MaxDeceleration" Value="2.0"/>
</Profile>

For further information, please refer to:

Treiber, Martin; Hennecke, Ansgar; Helbing, Dirk (2000), “Congested traffic states in empirical observations and microscopic simulations”, Physical Review E, 62 (2): 1805–1824, https://arxiv.org/pdf/cond-mat/0002177.pdf