Algorithm_Lateral
This module is responsible for the control of the vehicle’s lateral behavior. It converts the lateral input of the driver module into a steering wheel angle. The steering wheel angle can then be forwarded to a vehicle dynamics module like Dynamics_RegularDriving.
Detailed description of the module’s features
Algorithm_Lateral receives its command variables from a driver behavior model (or an ADAS) and generates the steering wheel angle of the driver to match these command variables. The steering wheel angle parts of all controllers are summed up to the overall steering wheel angle of the driver, which is then sent to a vehicle dynamics module like Dynamics_RegularDriving. The control loop is closed by the movement of the vehicle in the world, which is again monitored by the driver behavior model. This overall control loop of vehicle lateral guidance involving Algorithm_Lateral is illustrated in the following image with the following variables:
 is the actual curvature of the vehicle
is the actual curvature of the vehicle
Four variables containing the information needed for the open-loop controller:
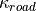 is the curvature at the front center (i.e. center of the front of the bounding box) of the ego vehicle. It uses the vectors:
is the curvature at the front center (i.e. center of the front of the bounding box) of the ego vehicle. It uses the vectors: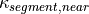 containing the curvatures of several segments starting at the front center up to 2m in front of the vehicles leading edge
containing the curvatures of several segments starting at the front center up to 2m in front of the vehicles leading edge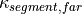 containing the curvatures of several segments starting 2m in front of the vehicle and ending 8m in front of it
containing the curvatures of several segments starting 2m in front of the vehicle and ending 8m in front of it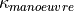 containing the curvature of the planned trajectory relative to the road
containing the curvature of the planned trajectory relative to the road
Other variables:
 is the actual lateral position of the vehicle in the road coordinate system
is the actual lateral position of the vehicle in the road coordinate system w is the lateral deviation
w is the lateral deviation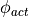 is the actual heading angle of the vehicle in the road coordinate system
is the actual heading angle of the vehicle in the road coordinate system
 is the heading error
is the heading error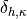 is the steering wheel angle from the curvature controller
is the steering wheel angle from the curvature controller is the steering wheel angle from the lateral deviation controller
is the steering wheel angle from the lateral deviation controller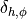 is the steering wheel angle from the heading error controller
is the steering wheel angle from the heading error controller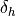 is the overall steering wheel angle of the driver
is the overall steering wheel angle of the driver
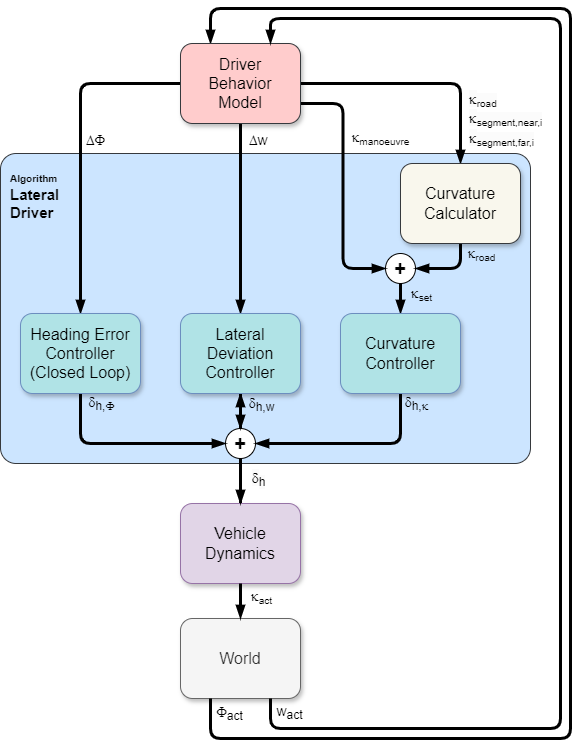
Components and signal flow of the lateral guidance control loop
The following subsections describe the theoretical background and the transfer functions of the different controllers.
Lateral dynamics
The lateral dynamics model is based on the Ackermann model which is a simple geometric
expression for the relationship between the steering angle at the front wheels and
the curvature the vehicle produces from it. It has several simplifications, where
the most notable is the reduction of the wheels of one axle to a single surrogate
wheel. This is suitable under the consideration that the steering angles of the front
wheels are rather small and do not differ much between the left and the right
front wheel. The first simplification may not hold up in city traffic with high
curvatures. Therefore the closed-loop-controller must have increased gains in
these situations. 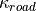 ,
, 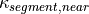 and
and 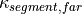 are smoothed and weighted before adding
are smoothed and weighted before adding 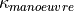 to form
to form  .
.
The Ackermann model is illustrated in the following image with the following variables:
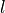 is the wheelbase of the vehicle
is the wheelbase of the vehicle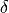 is the surrogate steering angle at the front wheels towards the vehicle’s longitudinal axis
is the surrogate steering angle at the front wheels towards the vehicle’s longitudinal axis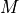 is the instantaneous centre of rotation, around which the vehicle is driving on a curve
is the instantaneous centre of rotation, around which the vehicle is driving on a curve is the radius of the curve, which the vehicle is driving around M
is the radius of the curve, which the vehicle is driving around M is the curvature of this curve, which is simply the inverse of r
is the curvature of this curve, which is simply the inverse of r
Illustration of the Ackermann model
In accordance to the current definitions of coordinate systems, the coordinate reference point of the vehicle is considered to be the rear axle center. Therefore, the curvature of the vehicle is also expressed towards the rear axle center and not to the centre of gravity, which is why the centre of gravity is not depicted in illustration of the Ackermann model.
The equation derived from the Ackermann model states the following
relation between the surrogate steering angle 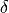 of the front wheels and
the curvature
of the front wheels and
the curvature  described by the rear axle around the instantaneous
centre of rotation
described by the rear axle around the instantaneous
centre of rotation 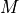 :
:
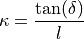
This equation can be inverted to express a required steering angle 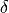 to
adjust a specific curvature
to
adjust a specific curvature  :
:

To convert this into the required steering wheel angle 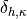 ,
the ratio
,
the ratio  of the steering gear must be applied:
of the steering gear must be applied:
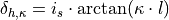
The vehicle parameters 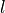 and
and  are received from the module Parameters_Vehicle.
are received from the module Parameters_Vehicle.
Heading controller
The heading controller is designed as a simple proportional controller.
The general transfer function of a P-controller with the input signal heading
error 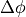 and the output signal steering wheel angle
and the output signal steering wheel angle 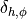 is described as:
is described as:
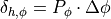
The controller amplification 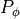 is therefore described as the
ratio between input signal and output signal:
is therefore described as the
ratio between input signal and output signal:
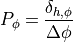
The controller amplification 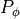 therefore expresses, how many
degrees of steering wheel angle are generated by one degree heading error.
The design of this controller amplification
therefore expresses, how many
degrees of steering wheel angle are generated by one degree heading error.
The design of this controller amplification 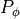 uses some
considerations about plane driving kinematics of Kramer. First of all,
the heading error
uses some
considerations about plane driving kinematics of Kramer. First of all,
the heading error 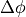 is derived from the current curvature
is derived from the current curvature  of the vehicle over the change of distance
of the vehicle over the change of distance 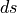 along the road’s longitudinal
coordinate
along the road’s longitudinal
coordinate  in one time step:
in one time step:
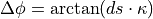
Under the consideration of small angular changes in one time step, this equation can be linearized to:
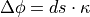
The curvature  of the vehicle can be substituted by an Ackermann model
(see here for further information about that):
of the vehicle can be substituted by an Ackermann model
(see here for further information about that):
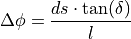
This equation can also be linearized under the consideration of small angles:
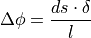
The connection to the steering wheel angle 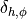 can be
applied by the ratio
can be
applied by the ratio  of the vehicle’s steering gear:
of the vehicle’s steering gear:
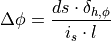
This equation can be transformed to a similar form as the controller’s transfer function above:
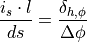
The usage of the incremental difference 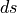 in this equation is problematic,
because the controller amplification becomes dependent on the simulation step
size. Because of this, the absolute change
in this equation is problematic,
because the controller amplification becomes dependent on the simulation step
size. Because of this, the absolute change 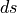 of the longitudinal road
coordinate
of the longitudinal road
coordinate  is substituted by the vehicle’s absolute velocity
is substituted by the vehicle’s absolute velocity  as a
simplification, which is the change of travelled distance with respect to time:
as a
simplification, which is the change of travelled distance with respect to time:
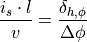
To tune the absolute influence of the heading controller in the overall control
loop, an additional gain factor 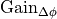 is applied to this
transfer function, which allows a situation dependent amplification of the
heading controller by the driver behavior model:
is applied to this
transfer function, which allows a situation dependent amplification of the
heading controller by the driver behavior model:
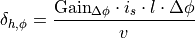
The vehicle parameters 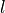 and
and  are received from the module Parameters_Vehicle, the vehicle’s
absolute velocity
are received from the module Parameters_Vehicle, the vehicle’s
absolute velocity  is received from the module Sensor_Driver,
and the additional controller gain
is received from the module Sensor_Driver,
and the additional controller gain 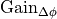 is received from
a driver behavior model.
is received from
a driver behavior model.
Lateral deviation controller
The lateral deviation controller is designed as a simple proportional controller. The general transfer
function of a P-controller with the input signal lateral deviation  w and
the output signal steering wheel angle
w and
the output signal steering wheel angle  is described as:
is described as:
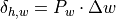
The controller amplification 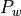 is therefore described as the ratio
between input signal and output signal:
is therefore described as the ratio
between input signal and output signal:
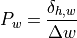
The controller amplification 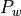 therefore expresses, how many degrees
of steering wheel angle are generated by one metre of lateral deviation. The
design of this controller amplification
therefore expresses, how many degrees
of steering wheel angle are generated by one metre of lateral deviation. The
design of this controller amplification 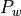 uses some considerations
about plane driving kinematics of Kramer. First of all, the lateral deviation
uses some considerations
about plane driving kinematics of Kramer. First of all, the lateral deviation
 w is derived from the current heading error
w is derived from the current heading error 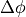 over the change
of distance
over the change
of distance 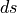 along the road’s longitudinal coordinate
along the road’s longitudinal coordinate  in one time step:
in one time step:
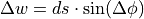
The current heading error 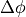 can further be substituted by an
expression of
can further be substituted by an
expression of 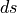 and the current curvature
and the current curvature  of the vehicle
(see Heading controller for that matter):
of the vehicle
(see Heading controller for that matter):

Under the consideration of small angular changes in one time step, this equation can be linearized to:
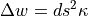
The curvature  of the vehicle can be substituted by an Ackermann model
(see here for further information about that):
of the vehicle can be substituted by an Ackermann model
(see here for further information about that):
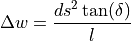
This equation can also be linearized under the consideration of small angles:
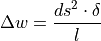
The connection to the steering wheel angle  can be applied
by the ratio
can be applied
by the ratio  of the vehicle’s steering gear:
of the vehicle’s steering gear:
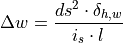
This equation can be transformed to a similar form as the controller’s transfer function above:
The usage of the incremental difference 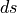 in this equation is problematic,
because the controller amplification becomes dependent on the simulation step
size. Because of this, the absolute change
in this equation is problematic,
because the controller amplification becomes dependent on the simulation step
size. Because of this, the absolute change 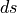 of the longitudinal road
coordinate
of the longitudinal road
coordinate  is substituted by the vehicle’s absolute velocity
is substituted by the vehicle’s absolute velocity  as a
simplification, which is the change of travelled distance with respect to time:
as a
simplification, which is the change of travelled distance with respect to time:
To tune the absolute influence of the lateral deviation controller in the
overall control loop, an additional gain factor 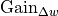 is
applied to this transfer function, which allows a situation dependent
amplification of the lateral deviation controller by the driver behavior model:
is
applied to this transfer function, which allows a situation dependent
amplification of the lateral deviation controller by the driver behavior model:
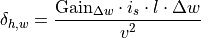
The vehicle parameters 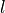 and
and  are received from the module Parameters_Vehicle, the vehicle’s
absolute velocity
are received from the module Parameters_Vehicle, the vehicle’s
absolute velocity  is received from the module Sensor_Driver,
and the additional controller gain
is received from the module Sensor_Driver,
and the additional controller gain 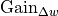 is received from a
driver behavior model.
is received from a
driver behavior model.