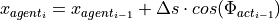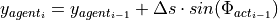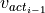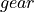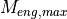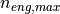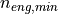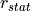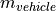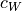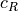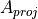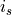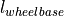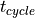Dynamics_RegularDriving
This module is responsible for the vehicle dynamics under normal driving conditions. It receives a signal from the lateral dynamics module Algorithm_Lateral containing the steering wheel angle. Accelerator pedal position, brake pedal position and the currently engaged gear are fetched from the signal sent by the longitudinal dynamics module Algorithm_Longitudinal. The module is using these inputs and the vehicle parameters from Parameters_Vehicle to determine the resulting vehicle speed, yaw angle and absolute position in the road coordinate system. The calculated values are passed on to the simulation framework/WorldObjectInterface.
Overview of the module’s functionalities
Longitudinal dynamics
The core element of all longitudinal calculations in this model are speed and acceleration. To determine the change of speed 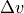 and the vehicles velocity
and the vehicles velocity 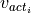 of the current time step
of the current time step 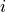 the actual acceleration
the actual acceleration 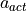 has to be known.
has to be known.
The module uses a simplified longitudinal dynamics model e.g. it doesn’t factor in rotational inertias.
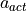 is dependend on the state variables and parameters shown in table 1.
is dependend on the state variables and parameters shown in table 1.
Variable |
Meaning |
Unit |
Source |
|---|---|---|---|
|
currently saved velocity of agent |
m/s |
WorldObjectInterface |
|
position of accelerator/brake pedal |
Algorithm_Longitudinal |
|
|
chosen gear |
Algorithm_Longitudinal |
|
|
gear ratio of current gear |
vehicleModelParameters |
|
|
gear ratio of axle |
vehicleModelParameters |
|
|
maximum torque of the vehicle engine |
Nm |
vehicleModelParameters |
|
maximum engine speed |
1/min |
vehicleModelParameters |
|
minimum engine speed |
1/min |
vehicleModelParameters |
|
static wheel radius |
m |
vehicleModelParameters |
|
vehicle mass |
kg |
vehicleModelParameters |
|
air drag coefficient |
vehicleModelParameters |
|
|
rolling resistance tire |
vehicleModelParameters |
|
|
front surface |
m² |
vehicleModelParameters |
First variables are used to calculate the current engine speed 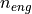 .
To do so the speed of the wheels
.
To do so the speed of the wheels 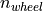 is determined via the vehicle velocity and static wheel radius:
is determined via the vehicle velocity and static wheel radius:
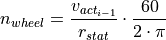
The powertrain model in the following image is used to further derive the engine speed 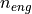 using the gear ratio
using the gear ratio 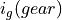 of the currently engaged gear and axle ratio
of the currently engaged gear and axle ratio 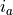 .
.
Illustration of the powertrain model and its parameters and state variables
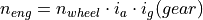
The maximum torque 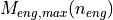 at the current engine speed is determined using the engine torque map shown in the following image:
at the current engine speed is determined using the engine torque map shown in the following image:
Simplified Engine Map
At this point the module differentiates between deceleration and acceleration by checking whether the value of 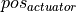 is positive or negative.
Negative values indicate the use of the brake pedal between 0-100% while positive values represent the use of the accelerator pedal.
is positive or negative.
Negative values indicate the use of the brake pedal between 0-100% while positive values represent the use of the accelerator pedal.
Driving resistance: There are driving resistances to be considered during the drive due to the rolling resistance of tires and air resistance which
could be calculated according to the follwing relations in fluid mechanics, where 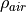 stands for air density in
stands for air density in 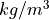 :
:
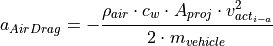
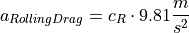
The rolling resistance of vehicle is currently set as a dummy value (0.0125), because the related value is not in the catalog of vehicle models yet and therefore it still can not be tapped in interface.
Decelerating: When decelerating 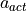 is the sum of the acceleration resulting from engine drag
is the sum of the acceleration resulting from engine drag 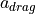 and acceleration from braking
and acceleration from braking 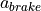 .
Whenever the driver is braking the module assumes that the engine is dragging with a moment equal to 10% of the maximum torque at the current engine speed.
.
Whenever the driver is braking the module assumes that the engine is dragging with a moment equal to 10% of the maximum torque at the current engine speed.
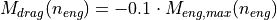
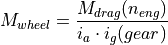
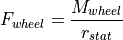
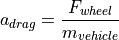
The maximum braking deceleration is set to 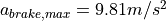 . The actual braking power is proportional to the position of the braking pedal.
. The actual braking power is proportional to the position of the braking pedal.
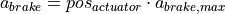
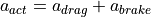
Acceleration: When the driver applies pressure on the accelerator the applied engine torque  is calculated as proportional to the accelerator pedal position and the span between engine drag and maximum engine torque
is calculated as proportional to the accelerator pedal position and the span between engine drag and maximum engine torque 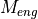 (
(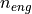 ) at the current engine speed.
) at the current engine speed.
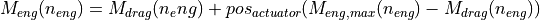
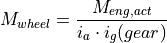
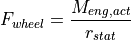
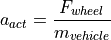
Once the acceleration of the vehicle is known the change in velocity is determined by its discrete time integral.
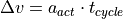
The sum of the previous velocity and change in velocity result in the actual vehicle velocity of the current time step:
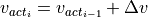
Lateral dynamics
The lateral dynamics model is based on the Ackermann model which reduces the steering kinematics to a single surrogate front wheel. Considering the relatively small steering angles when driving on the highway this simplification is deemed suitable. The heading is updated using the previous heading and the change in yaw due to the steering wheel angle which is converted into a yaw rate using the simplified Ackermann model shown in the following image.
Illustration of the Ackermann model
Variable |
Meaning |
Unit |
Source |
|---|---|---|---|
|
steering wheel angle |
rad |
Algorithm_Lateral |
|
heading at previous time step |
rad |
WorldObjectInterface |
|
steering ratio |
vehicleModelParameters |
|
|
wheelbase |
m |
vehicleModelParameters |
|
distance travelled since last time step |
m |
previously calculated in the module |
|
cycle time |
ms |
ModelInterface |
The steering wheel angle 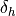 is proportional to the front wheel angle
is proportional to the front wheel angle 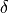 :
:
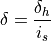
The Ackermann model provides the geometric connection between the front wheel angle and the resulting curvature  :
:
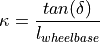
The combination of curvature  and driven distance at that curvature
and driven distance at that curvature 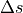 result in the change of the heading
result in the change of the heading 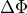 :
:
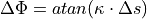
The new heading 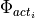 is the old heading
is the old heading 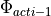 plus the previously calculated change in heading
plus the previously calculated change in heading 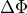 :
:
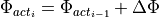
Updating position
Once the new vehicle speed 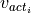 is determined the distance travelled during the last timestep
is determined the distance travelled during the last timestep 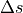 is determined:
is determined:
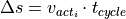
Using the actual vehicle yaw angle in the road coordinate 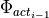 the vehicles new x- and y-coordinates are calculated:
the vehicles new x- and y-coordinates are calculated: