Longitudinal and Lateral Control
Driving behaviour in SCM is mainly characterised by lateral and longitudinal actions. The following chapter provides an overview on how speed and following distances are adjusted, how the lane keeping action works and also explains the special case of behaviour in traffic jams and how emergency lanes are considered.
Speed Adjustment
The set value of longitudinal acceleration is used in case of the action speed adjustment to regulate the target speed of the driver.
For all other actions, it is a limited value for the calculation of accelerations, so that the own target speed will never be overridden.
The calculation of the set value for acceleration 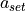 is dependent on the target speed
is dependent on the target speed  and the current speed of the agent
and the current speed of the agent 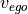 :
:
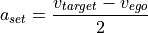
The calculated values of 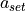 have an upper limit given by the comfort longitudinal acceleration and a lower one by the comfort longitudinal deceleration (see ParametersAgent).
have an upper limit given by the comfort longitudinal acceleration and a lower one by the comfort longitudinal deceleration (see ParametersAgent).
Following Distance
The car following behaviour is divided into three different longitudinal actions:
approaching a vehicle that can be followed
following another vehicle at a desired distance
falling back to the desired following distance when too close to the vehicle ahead
Approaching describes the behaviour between InfluencingDistance and EquilibriumDistance.
The set value of acceleration during approaching 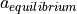 is realized as a target braking to EquilibriumDistance.
is realized as a target braking to EquilibriumDistance.
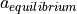 is the sum of three parts:
is the sum of three parts:
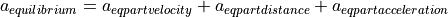
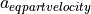 is defined as follows:
is defined as follows:
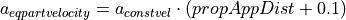
propAppDist is defined as the propotional value for the approaching case.
It is calculated by the 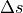 with respect to the reduction factor for following distance and the distance to regulate
with respect to the reduction factor for following distance and the distance to regulate 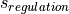 .
.
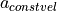 is a function of
is a function of 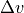 to leading vehicle and
to leading vehicle and 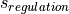 :
:
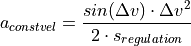
The 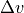 for the approaching case is with respect to the situation always in consideration.
It is calculated with a gain of 25% of the
for the approaching case is with respect to the situation always in consideration.
It is calculated with a gain of 25% of the 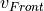 , where the tolerance area of the value ranges from 10 km/h to 25 km/h.
The
, where the tolerance area of the value ranges from 10 km/h to 25 km/h.
The 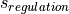 is calculated with the parameters reactionBaseTimeMean and pedalChangeTimeMean (Driver Parameters):
is calculated with the parameters reactionBaseTimeMean and pedalChangeTimeMean (Driver Parameters):
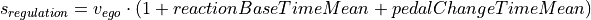
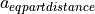 and
and 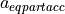 are defined as follows:
are defined as follows:


In this case, the 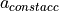 is equal to the acceleration of the observed vehicle.
is equal to the acceleration of the observed vehicle.
The actions of following at and falling back to a desired distance describe the actual following behaviour of the vehicle.
Here, the following distance is regulated to approach the EquilibriumDistance.
For the calculation of the set value of accelaration 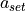 , the Wiedemann model is used in both cases.
It is composed of three different acceleration values:
, the Wiedemann model is used in both cases.
It is composed of three different acceleration values:
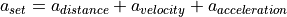
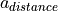 serves as a function of the current relative distance
serves as a function of the current relative distance 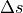 to the leading vehicle, the EquilibriumDistance
to the leading vehicle, the EquilibriumDistance 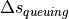 and the maximal amount of the acceleration
and the maximal amount of the acceleration 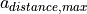 for the pure distance regulation:
for the pure distance regulation:
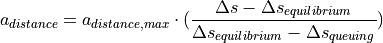
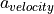 is a function of the current relative velocity
is a function of the current relative velocity 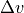 to the leading vehicle, the current relative distance
to the leading vehicle, the current relative distance 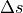 to leading vehicle and the queuing distance
to leading vehicle and the queuing distance 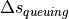 :
:
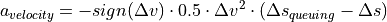
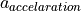 is equal to the accelaration
is equal to the accelaration 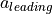 of the leading vehicle:
of the leading vehicle:
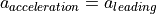
The differentiation between following and falling back only exists in the value used in the calculations, the parameterization and the permitted value ranges for the calculated value 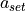 :
(The behavioral parameters are explained in Driver Parameters.)
:
(The behavioral parameters are explained in Driver Parameters.)
following at a desired distance |
falling back to the desired distance |
|
|---|---|---|
used values |
|
|
value for |
comfortLongitudinalDeceleration |
maximumLongitudinalDeceleration |
upper value for |
comfortLongitudinalAcceleration |
decelerationFromPowertrainDrag |
botttom value for |
comfortLongitudinalDeceleration |
maximumLongitudinalDeceleration |
Time To Collision
The time to collision (TTC) is a time-based measure to track collision courses of two ore more objects. The TTC measure makes the modeling of human behaviour in SCM possible. Real-world data can be used to parametrise the simulation model.
Time To Brake
Target braking
The set value of longitudinal accelaration for a target braking is calculated in case of the longitudinal action of braking to the end of the lane.
The calculation of the set accelaration 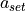 depends on the agent’s current velocity
depends on the agent’s current velocity 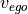 and the current relative distance
and the current relative distance 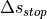 to the target point on the road:
to the target point on the road:
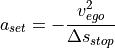
The calculated values of 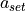 are limited to stay between the comfort longitudinal deceleration and the maximum longitudinal deceleration (see Driver Parameters).
are limited to stay between the comfort longitudinal deceleration and the maximum longitudinal deceleration (see Driver Parameters).
Lane Centering
Command variable calculations for lateral guidance
The command variables of the lateral control are the set course curvature 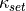 , the course angle error
, the course angle error 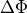 and the lateral deviation
and the lateral deviation 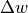 with respect to the set trajectory.
The set course curvature
with respect to the set trajectory.
The set course curvature 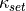 is constantly calculated from the current course curvature
is constantly calculated from the current course curvature 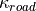 and the planned course curvature
and the planned course curvature 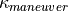 from the current driving maneuver:
from the current driving maneuver:
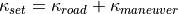
The controlling deviations 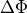 and
and 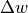 are the respective difference between set and actual value:
are the respective difference between set and actual value:
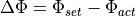
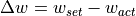
The actual values refer to the road coordinate system and are queried earlier.
The necessary values for the set values 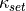 ,
, 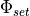 and
and 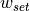 are calculated depending on the current lateral action.
Gains of the regulation
are calculated depending on the current lateral action.
Gains of the regulation 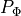 and
and 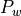 are currently constant (
are currently constant (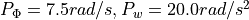 ).
).
Lane keeping
The lateral control for lane keeping is applied for the lateral actions lane keeping, intent to change lanes and planned merging maneuver.
The set values 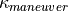 ,
, 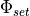 and
and 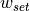 mentioned earlier are constant at 0 due to the fact that the maneuver only follows the course of the road.
This has the following consequences for the output values of the lateral control in case of lane keeping:
mentioned earlier are constant at 0 due to the fact that the maneuver only follows the course of the road.
This has the following consequences for the output values of the lateral control in case of lane keeping:
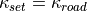
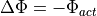
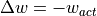
Lateral positioning
The neutral lateral position, i.e. the lateral position the agent tries to reach with respect to the lane center, is determined individually for each agent. It can be manipulated through the lateralOffsetNeutralPosition-parameters. Currently the offset from the lane center only applies to vehicles in queued traffic (below jam velocity). Therefore, the actual lateral offset is not suddenly applied at jam velocity but ramps up to reach its full value at 20 km/h below jam velocity.
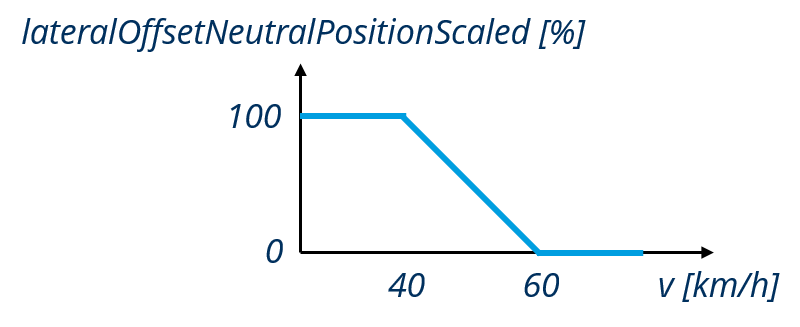
Fig. 35 Lateral offset neutral position scaled
Since this is the driver’s desired lateral positioning, it is also considered for all other lateral maneuvers, such as lane changes, swerving etc. The maneuver will end at that specific lateral offset.
Traffic Jam Behaviour
Emergency lane
Depending on road type and country specific criteria, agents will form a rescue lane when traffic gets close to a standstill (below 10 km/h). This applies to agents on the left most lane, where they move to the left side of the lane and its right neighbouring lane, where vehicles move to the right. This behaviour, consisting of the amount of lateral displacement from the lane center and the compliance quota (cooperative behaviour) can be manipulated via the corresponding parameters. This mechanic supersedes the lateral positioning mentioned above and will lead to an extended final lateral position as seen below.
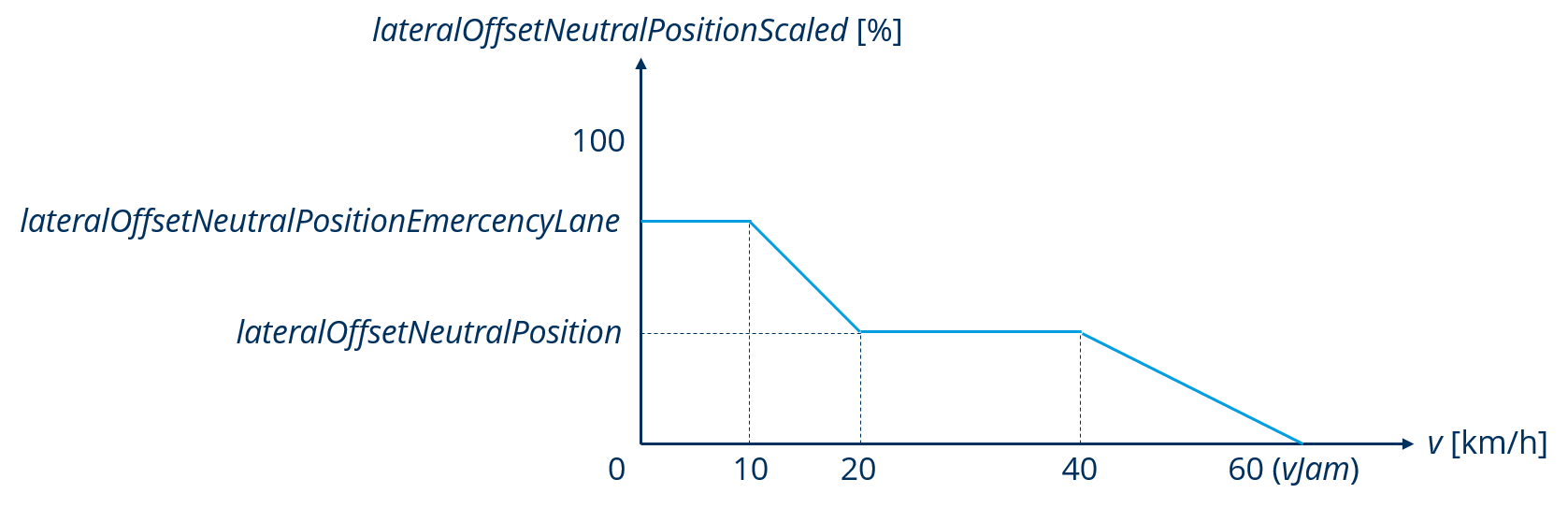
Fig. 36 Lateral offset neutral position scaled with emergency lane (vJam - jam velocity)
There is also a linear ramp up between 20 and 10 km/h to avoid big sudden changes for the lateral controller.
Note: The current implementation always considers the road to be a motorway and the country specific rules to require the formation of a rescue lane.