Tau Theory
Visual perception within SCM draws on the so-called Tau theory by David N. Lee (1976). The theory is based on geometric considerations, how humans are able to visually perceive time related values such as the TTC or time headway to an object. Fundamental assumptions of Tau theory are summarized in the first subsection of this chapter. Further explanations on how this theory is implemented in SCM are given in the second subsection.
Fundamentals of the Tau Theory according to Lee
Lee regards the monocular optical projection of environmental objects on the retina as projections through a pinhole (pupil) on the inside of a sphere with unit radius (retina). This constitutes the following simplifications:
the projection occurs through the centre of the lens
the retina depicts a sphere and its radius is negligibly small compared to the distance from the object
For modelling purposes, the retinal projection of a real world object must be simplified and can be considered by two arbitrary points on the object’s surface.
In general, this information is provided by the object’s outlines, which can be further simplified and described by the object’s width or height.
The geometrical relations by means of an environmental object obj of width 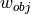 along the visual axis
along the visual axis 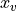 are shown in Fig. 18
are shown in Fig. 18
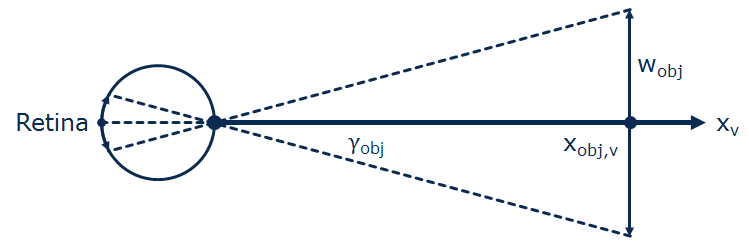
Fig. 18 Retinal projection of an environmental object obj of width w_obj along the visual axis x_v
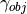 constitutes the retinal size of the projection of
constitutes the retinal size of the projection of 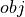 in terms of its real width
in terms of its real width 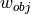 .
It can be expressed by the angular relations of the two right-angled triangles:
.
It can be expressed by the angular relations of the two right-angled triangles:

Declaring that 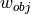 is much smaller than the relative distance
is much smaller than the relative distance 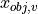 to the object
to the object 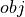 , this can be simplified to:
, this can be simplified to:
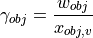
In case of a relative motion between eye and object 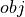 , the relative distance
, the relative distance 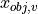 changes by the relative velocity
changes by the relative velocity 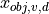 , while the object’s real size
, while the object’s real size 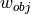 remains constant.
The angular change
remains constant.
The angular change 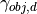 of the retinal size
of the retinal size 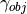 is given by the time derivative of the equation above:
is given by the time derivative of the equation above:
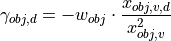
The above equation converted to 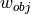 and substituted in the equation before that reveals:
and substituted in the equation before that reveals:
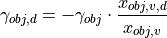
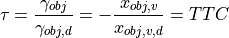
The right side of the equation above complies with the definition of the time to collision 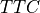 .
The relative distance
.
The relative distance 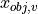 is greater than 0 until colliding with the object
is greater than 0 until colliding with the object 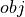 .
In case of an approach,
.
In case of an approach, 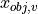 decreases and
decreases and 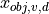 is smaller than 0.
According to the equation, the TTC is greater than 0 in that case.
Contrary to that, a negative TTC indicates a motion away from object
is smaller than 0.
According to the equation, the TTC is greater than 0 in that case.
Contrary to that, a negative TTC indicates a motion away from object 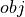 .
The border case constitutes a relative velocity
.
The border case constitutes a relative velocity 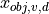 equal 0, which induces an infinite TTC.
From a physical point of view, that definition appears to be valid, because in case of a non-existent relative motion, an infinite amount of time is going to pass until a collision with the object
equal 0, which induces an infinite TTC.
From a physical point of view, that definition appears to be valid, because in case of a non-existent relative motion, an infinite amount of time is going to pass until a collision with the object 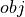 occurs.
occurs.
What the equation further reveals is the fact that the human eye can most likely perceive the TTC to an object 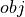 simply by detecting the kinematical changes of its retinal projection.
To distinguish between kinematical and optical terms, Lee defined the left side of the equation as the optical variable
simply by detecting the kinematical changes of its retinal projection.
To distinguish between kinematical and optical terms, Lee defined the left side of the equation as the optical variable 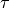 (Tau).
(Tau).
According to Lee, humans do not solely use the physiological perception of the TTC in the form of the optical variable 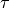 for coordinating visual-motoric tasks, especially when the relative motion is not determined by a constant relative velocity
for coordinating visual-motoric tasks, especially when the relative motion is not determined by a constant relative velocity 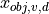 , but a relative acceleration
, but a relative acceleration 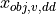 .
In those cases, the simple consideration of a temporal value of
.
In those cases, the simple consideration of a temporal value of 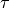 would generate an incomplete picture of how the situation evolves.
would generate an incomplete picture of how the situation evolves.
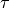 expresses the time left until colliding with object
expresses the time left until colliding with object 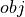 , but that amount of time is only correct, if the relative velocity
, but that amount of time is only correct, if the relative velocity 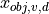 does not change over that period.
If there is any change in
does not change over that period.
If there is any change in 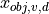 , the actual time until a collision can be much greater or smaller than the value expressed by
, the actual time until a collision can be much greater or smaller than the value expressed by 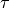 .
.
Lee postulates that the human eye uses the time derivative 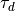 of the optical variable
of the optical variable 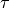 for considering a relative acceleration
for considering a relative acceleration 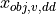 .
.
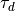 describes the gradient of the TTC and therefore clarifies the urgency of the situation’s evolvement, assuming that the relative acceleration
describes the gradient of the TTC and therefore clarifies the urgency of the situation’s evolvement, assuming that the relative acceleration 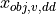 remains constant.
It can be concatenated with the values of relative motion by deriving
remains constant.
It can be concatenated with the values of relative motion by deriving 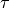 with respect to time:
with respect to time:
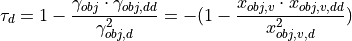
It is commonly known that a perception threshold 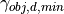 of the human eye exists for the expansion rate
of the human eye exists for the expansion rate 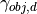 .
This leads to certain consequences in the perceptibility of the optical variable
.
This leads to certain consequences in the perceptibility of the optical variable 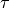 .
At first,
.
At first, 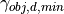 is declared as a constant and substituted for
is declared as a constant and substituted for 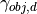 .
By converting the equation for
.
By converting the equation for 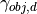 to
to 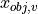 and substituting that into the equation for
and substituting that into the equation for 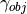 , the relative distance
, the relative distance 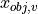 to the object can firstly be eliminated from the equation system:
to the object can firstly be eliminated from the equation system:
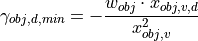
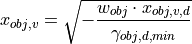
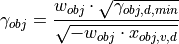
The last equation and substituting 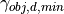 again in the equation for
again in the equation for 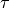 finally reveals an expression for the perception threshold
finally reveals an expression for the perception threshold 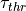 of the optical variable
of the optical variable 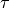 :
:
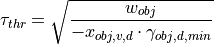
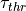 is an upper bound of perception.
For all values of the optical variable
is an upper bound of perception.
For all values of the optical variable 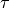 that are greater than
that are greater than 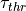 respectively smaller than
respectively smaller than 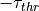 , the human eye is not able to perceive
, the human eye is not able to perceive 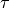 .
Its value can be regarded as infinite in those cases (within SCM, the maximum value of
.
Its value can be regarded as infinite in those cases (within SCM, the maximum value of 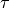 is set at 99.0 s).
is set at 99.0 s).
For further information, please see Lee’s original paper:
Lee, D. N. (1976). A theory of visual control of braking based on information about time-to-collision. Perception, 5 (4), 437-459.
Implementation of the Tau Theory in SCM
The calculation formulas described previously are utilized for the calculation of 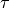 (perceive the TTC) and
(perceive the TTC) and 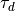 (perceive the time derivate of Tau, i.e. the change gradient of the TTC).
The perceptibility of
(perceive the time derivate of Tau, i.e. the change gradient of the TTC).
The perceptibility of 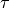 expressed by the perception threshold
expressed by the perception threshold 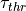 is checked against the observed object’s width and height, considering the given relative velocity.
If
is checked against the observed object’s width and height, considering the given relative velocity.
If 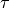 (calculated by the given relative distance and relative velocity) can be perceived in either direction, it is returned by the function.
Otherwise, the maximum possible value of 99.0 s is returned.
(calculated by the given relative distance and relative velocity) can be perceived in either direction, it is returned by the function.
Otherwise, the maximum possible value of 99.0 s is returned.
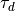 can only be perceived, if
can only be perceived, if 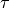 itself is perceivable.
The perception threshold
itself is perceivable.
The perception threshold 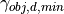 for the necessary expansion rate of the retinal projection is provided by the driver parameters.
There are two different threshold values regarding foveal perception or perception in the UFOV (see Gaze Control for further explanations).
for the necessary expansion rate of the retinal projection is provided by the driver parameters.
There are two different threshold values regarding foveal perception or perception in the UFOV (see Gaze Control for further explanations).
According to Lee, the mechanism for the perception of the TTC can also be transferred to the perception of the time headway. This is done for the time headway (perceive the gap) and its time derivative (perceive the gap changing rate). As Lee does not provide any approaches for the modelling of perception thresholds of the time headway, these functions always return a valid value for their respective variables. The functions take reasonable considerations about the positioning of the observed object and the driver’s own vehicle, because the time headway is always measured from the following vehicle.
Applying the Tau theory, SCM considers longitudinal as well as lateral movements for its calculations.
Tau’s time derivate 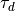 for lateral movements is an exception, since there is no lateral relative acceleration available for a calculation.
for lateral movements is an exception, since there is no lateral relative acceleration available for a calculation.