AlgorithmLongitudinalDriver
This module is responsible for the control of the vehicle’s longitudinal dynamics. It receives the command variables from a driver behaviour model like Implementation Architecture and generates the accelerator and brake pedal position and the current gear of the driver to match these command variables. The pedal positions and the gear have than to be send to a vehicle dynamics module like DynamicsRegularDriving. The actuation of the clutch pedal is currently not simulated by the module.
Overview of the module’s functionalities
AlgorithmLongitudinalDriver models human longitudinal guidance according to the two-level-model of vehicle guidance from Donges. It is the original form of his later three-level-model of vehicle guidance, which is expressing driver behaviour in a more phenomenological context, and was developed as part of Donges’ Ph.D. thesis (Donges only focussed on lateral guidance in this work, which is the base for the algorithms in AlgorithmLateralDriver; the phenomenology behind this model is transferred to longitudinal guidance in AlgorithmLongitudinalDriver). The model takes two overlapping mechanisms of human behaviour in human-machine-interactions into account:
Anticipatory open-loop control on guidance level: Every driver has knowledge about how his vehicle works, which is based on driving experience and familiarity with the vehicle. This can be expressed as a mental model representation about the vehicle. If the driver formulates a desired acceleration, he can use his knowledge about the vehicle to estimate, how much he has to press the accelerator pedal, so the vehicle’s powertrain generates the desired acceleration. This is a typically open-loop control process, where the mental representation of the vehicle represents a feedforward control, which generates a pedal position according to a desired acceleration, but the actual acceleration, which is produced by the vehicle, is not monitored. The better the mental model of the vehicle is, the better is this feedforward control, but even the best mental model cannot take into account external disturbances like slope. For influences like this, a second underlying control mechanism is needed.
Compensatory closed-loop control on stabilization level: As already mentioned above, the guidance level cannot take into account any external disturbance, because an open-loop control does not monitor the difference between command variable and its corresponding system state. For this reason (and to compensate the driver’s necessarily imperfect mental model about his vehicle), an underlying closed-loop control is needed. For instance, a driver is driving at his target speed on a plane road, which means that the required acceleration to reach his target speed is equal zero. In this case, the guidance level will also produce an accelerator pedal position equal to zero engine torque (compensation of powertrain drag can be part of the anticipatory open-loop control, if the driver’s mental model is sophisticated enough). If an external disturbance like a slope occurs, the state of the anticipatory level will not change, because this kind of driving resistance cannot be addressed by a feedforward control. The vehicle will of cause start to decelerate and therefore deviate from the target speed of the driver, which must be compensated by a closed-loop control that monitors the actual velocity of the vehicle.
Contrary to lateral guidance (AlgorithmLateralDriver), longitudinal guidance of a passenger car requires the actuation of two pedals, namely accelerator and brake pedal. As these two are furthermore controlled with the same foot, there is a necessary pedal change time when switching between pedals, which is modelled as a stochastic delay in the module’s signal chain.
AlgorithmLongitudinalDriver is currently modelled for the control of vehicles with manual transmissions, which incorporates an algorithm for the selection of the optimal gear. The actuation of a clutch pedal is not simulated by the module.
Detailed description of the module’s features
AlgorithmLongitudinalDriver receives its command variables from a driver behaviour model like Implementation Architecture and generates the pedal positions and the gear of the driver to match these command variables. The pedal positions of all controllers are summed up to the overall pedal position of the driver, which is complemented by a maybe necessary pedal change time and is than send to a vehicle dynamics module like DynamicsRegularDriving. The pedal positions within the module’s algorithms are defined as double values between -1 and 1, where values between 0 and 1 indicate accelerator actuation and values below 0 indicate brake pedal actuation. This is split up into two seperate output signals for accelerator and brake pedal by the function UpdateOutputParameters, but it makes handling inside the algorithms much easier. The gear is calculated within the inverted vehicle model of the open-loop controller. The control loop is closed by the movement of the vehicle. This overall control loop of vehicle longitudinal guidance involving AlgorithmLongitudinalDriver is illustrated in Fig. 52 with the following variables:
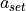 is the desired acceleration of the vehicle
is the desired acceleration of the vehicle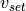 is the desired velocity of the vehicle, which is
is the desired velocity of the vehicle, which is 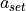 integrated over time
integrated over time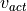 is the actual velocity of the vehicle
is the actual velocity of the vehicle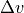 is the velocity error
is the velocity error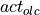 is the pedal position signal from the acceleration controller
is the pedal position signal from the acceleration controller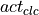 is the pedal position signal from the velocity controller
is the pedal position signal from the velocity controller is the overall pedal position of the controllers
is the overall pedal position of the controllers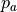 is the output signal for the accelerator pedal position
is the output signal for the accelerator pedal position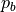 is the output signal for the brake pedal position
is the output signal for the brake pedal position is the current gear of the driver
is the current gear of the driver
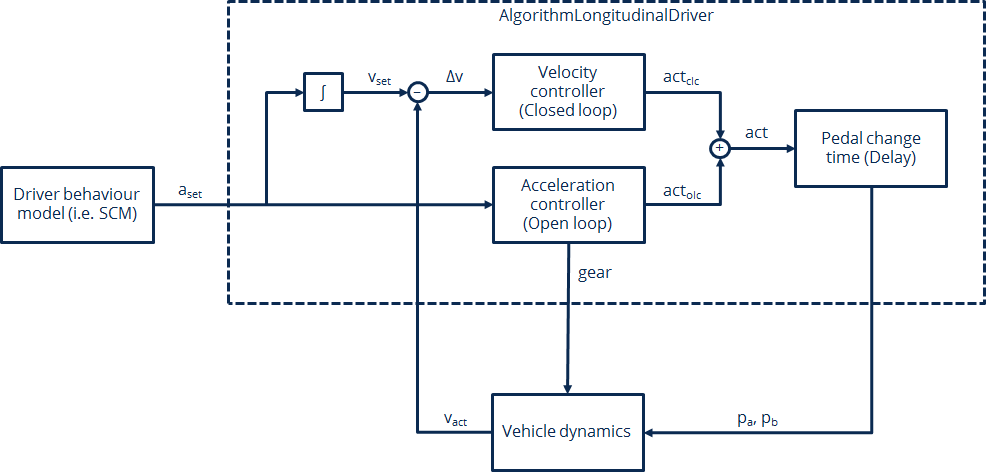
Fig. 52 Components and signal flow of the longitudinal guidance control loop
The following subsections describe the theoretical background and the transfer functions of the different controllers.
Anticipatory control on guidance level
As described in the overview section,
the driver’s controls on guidance level are characterized by anticipatory
mechanisms regarding the expected vehicle’s behaviour. In terms of control
theory and longitudinal guidance, this is modelled as an open-loop feedforward
controller, which generates an estimated pedal position 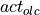 that
fits a required acceleration
that
fits a required acceleration 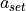 from the driver behaviour model.
This model-predictive controller is modelled as an inverted longitudinal
dynamics model of the vehicle’s powertrain and brake system. In terms of control
theory, this is a complex proportional controller, which is further complemented
by a first order transient behaviour. Therefore, the whole anticipatory
open-loop controller can be interpreted as a
from the driver behaviour model.
This model-predictive controller is modelled as an inverted longitudinal
dynamics model of the vehicle’s powertrain and brake system. In terms of control
theory, this is a complex proportional controller, which is further complemented
by a first order transient behaviour. Therefore, the whole anticipatory
open-loop controller can be interpreted as a 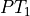 unit. The inverted
longitudinal dynamics model also includes an algorithm for the selection of the
optimal gear, regarding the required torque on the wheels to generate
unit. The inverted
longitudinal dynamics model also includes an algorithm for the selection of the
optimal gear, regarding the required torque on the wheels to generate 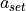 . The several aspects of this model are described below.
. The several aspects of this model are described below.
Inverted longitudinal dynamics model
The inverted longitudinal dynamics model produces the proportional part  of the open-loop acceleration controller by utilizing an inverted powertrain and
brake system model (see here for the application of the transient behaviour to calculate
of the open-loop acceleration controller by utilizing an inverted powertrain and
brake system model (see here for the application of the transient behaviour to calculate 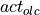 from
from  ). The powertrain model and all of its parameters and
state variables are illustrated in Fig. 53. The brake model is not worth
illustrating, as it directly applies on the required acceleration
). The powertrain model and all of its parameters and
state variables are illustrated in Fig. 53. The brake model is not worth
illustrating, as it directly applies on the required acceleration 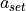 of the vehicle.
of the vehicle.
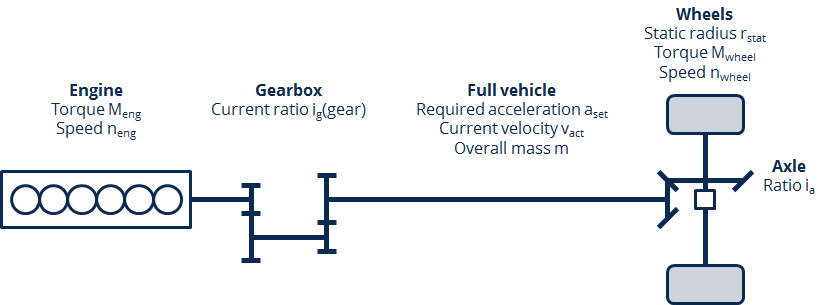
Fig. 53 Illustration of the powertrain model and its parameters and state variables
The core element of all calculations in this model is speed and acceleration.
The speed 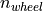 at the wheels is constraint by the current velocity
at the wheels is constraint by the current velocity
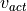 of the vehicle and the static wheel radius
of the vehicle and the static wheel radius 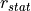 :
:
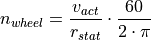
where 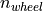 is defined in rotations/min and
is defined in rotations/min and 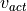 is
defined in m/s, which requires the conversion term at the end of the equation.
As the equation also illustrates, only a simple rolling relation defines the
model and there is no simulation of tire-road-friction and tire slip involved.
is
defined in m/s, which requires the conversion term at the end of the equation.
As the equation also illustrates, only a simple rolling relation defines the
model and there is no simulation of tire-road-friction and tire slip involved.
The speed 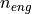 of the engine is constraint by the speed
of the engine is constraint by the speed
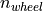 of the wheels, the ratio
of the wheels, the ratio  of the axle, and the
current ratio
of the axle, and the
current ratio 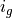 of the gearbox, depending of the current gear:
of the gearbox, depending of the current gear:
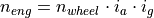
The required acceleration 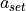 determines the torque
determines the torque 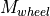 at the wheels, as the overall mass
at the wheels, as the overall mass 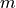 of the vehicle has to be accelerated by
this torque:
of the vehicle has to be accelerated by
this torque:
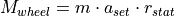
As the equation illustrates, no driving resistances other than the inertia of
the vehicle are simulated by this model. The required torque 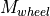 at the wheels must be generated by the engine, considering the ratios of the
powertrain:
at the wheels must be generated by the engine, considering the ratios of the
powertrain:
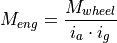
As the current speed 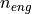 of the engine, the required acceleration
of the engine, the required acceleration
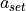 of the vehicle, and the required torque
of the vehicle, and the required torque 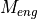 of the
engine are known or defined by the above equations, this knowledge can be used
to determine the estimated positions of the accelerator and the brake pedal or
to calculate the optimal gear for the required acceleration
of the
engine are known or defined by the above equations, this knowledge can be used
to determine the estimated positions of the accelerator and the brake pedal or
to calculate the optimal gear for the required acceleration 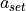 ,
if a positive acceleration is needed. For the accelerator pedal and optimal gear
calculation, there is still some missing knowledge about the engine itself.
The relationship between the current engine speed
,
if a positive acceleration is needed. For the accelerator pedal and optimal gear
calculation, there is still some missing knowledge about the engine itself.
The relationship between the current engine speed 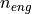 and the
possible engine torque
and the
possible engine torque 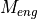 is determined by a simple engine map,
which is illustrated in Fig. 54:
is determined by a simple engine map,
which is illustrated in Fig. 54:
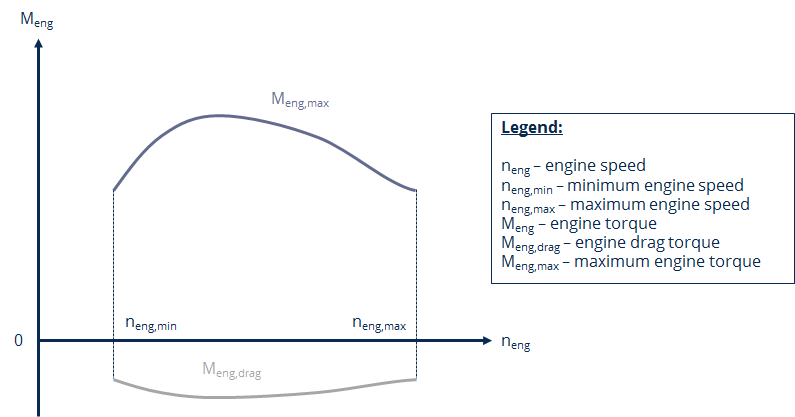
Fig. 54 Simplified engine map used for the inverted powertrain model
The engine map is defined by two characteristic curves:
 defines the maximum torque, which can be produced by the
engine at a specific engine speed
defines the maximum torque, which can be produced by the
engine at a specific engine speed 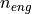 . This is directly connected
with the maximum possible actuation of the accelerator pedal.
. This is directly connected
with the maximum possible actuation of the accelerator pedal.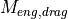 defines the drag torque, which is produced by the engine
at a specific engine speed
defines the drag torque, which is produced by the engine
at a specific engine speed 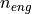 , if the accelerator pedal is not
actuated at all.
, if the accelerator pedal is not
actuated at all.
The two characteristic curves are only defined between the minimum and maximum
possible speed of the engine. As the two characteristic curves are directly
related to a full actuation (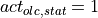 ) and no actuation
(
) and no actuation
(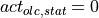 ) of the accelerator pedal, the estimated pedal
position for the accelerator pedal
) of the accelerator pedal, the estimated pedal
position for the accelerator pedal  , which produces the
currently required engine torque
, which produces the
currently required engine torque 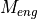 , can be calculated by linear
interpolation between these two characteristic curves at the current engine
speed
, can be calculated by linear
interpolation between these two characteristic curves at the current engine
speed 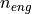 .
.
The same thing is done for the calculation of the estimated brake pedal position:
The maximum acuation of the brake pedal (
 ) is
directly connected with the maximum possible deceleration of the vehicle, which
is simply set to 1G (
) is
directly connected with the maximum possible deceleration of the vehicle, which
is simply set to 1G (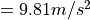 ).
).No actuation of the brake pedal (
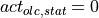 ) also produces no
deceleration.
) also produces no
deceleration.
Between these two possible decelerations, the estimated brake pedal position to
produce the required acceleration 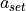 is calculated by linear
interpolation.
is calculated by linear
interpolation.
The logic for the calculation of the static controller output  ,
utilizing the considerations above, is defined as follows:
,
utilizing the considerations above, is defined as follows:
If the required acceleration 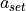 is smaller than zero, it can be
produced by the engine drag torque or the brake system. If the engine drag
torque
is smaller than zero, it can be
produced by the engine drag torque or the brake system. If the engine drag
torque 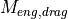 at the current engine speed
at the current engine speed 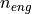 is not
strong enough to meet the engine torque
is not
strong enough to meet the engine torque 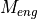 , which would be
necessary to produce
, which would be
necessary to produce 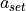 , an additional actuation of the brake
pedal is applied (the driver does not open the clutch, so the engine drag torque
is also applied to the wheels). This mechanism is not considering a change in
gears, but uses the current gear of the gearbox (the driver does not consider to
shift down for a stronger effect of the engine drag torque).
, an additional actuation of the brake
pedal is applied (the driver does not open the clutch, so the engine drag torque
is also applied to the wheels). This mechanism is not considering a change in
gears, but uses the current gear of the gearbox (the driver does not consider to
shift down for a stronger effect of the engine drag torque).
If the required acceleration 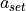 is greater than or equal to zero,
it can only be produced by the powertrain. First of all, the optimal gear to
produce the engine torque
is greater than or equal to zero,
it can only be produced by the powertrain. First of all, the optimal gear to
produce the engine torque 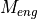 required for
required for 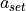 is
calculated, which is described in the subsequent subsection.
With this chosen gear, the current engine speed
is
calculated, which is described in the subsequent subsection.
With this chosen gear, the current engine speed 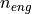 is calculated.
is calculated.
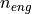 is used to determine the maximum engine torque
is used to determine the maximum engine torque  and the engine drag torque
and the engine drag torque 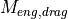 from the characteristic curves.
As these two values are connected to a full actuation and no actuation of the
accelerator pedal, the estimated accelerator pedal position, which is necessary
to produce the required acceleration
from the characteristic curves.
As these two values are connected to a full actuation and no actuation of the
accelerator pedal, the estimated accelerator pedal position, which is necessary
to produce the required acceleration 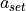 , can be calculated by
linear interpolation.
, can be calculated by
linear interpolation.
The state variable 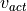 is received from the module SensorDriver,
the required acceleration
is received from the module SensorDriver,
the required acceleration 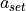 is received from a driver behaviour
model like Implementation Architecture , and the
vehicle parameters m,
is received from a driver behaviour
model like Implementation Architecture , and the
vehicle parameters m, 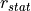 ,
, 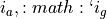 per gear,
and the information about the engine map are received from the module ParametersAgent.
per gear,
and the information about the engine map are received from the module ParametersAgent.
The calculations above are done in the function PedalPosition of the sub-module ALongitudinalDataProvider, which is called in the function CalculatePedalPositionAndGear of AlgorithmLongitudinalDriver.
Algorithm for optimal gear determination
The algorithm for the determination of the optimal gear for the required
acceleration 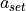 is implemented in the function GetBestGear of the
sub-module ALongitudinalDataProvider. It is called within the function
PedalPosition of the same sub-module, which applies the inverted longitudinal dynamics model
for the open-loop acceleration controller. The algorithm receives the current
velocity
is implemented in the function GetBestGear of the
sub-module ALongitudinalDataProvider. It is called within the function
PedalPosition of the same sub-module, which applies the inverted longitudinal dynamics model
for the open-loop acceleration controller. The algorithm receives the current
velocity 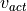 of the vehicle and the required acceleration
of the vehicle and the required acceleration 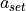 .
.
Within a for-loop over all gears, the engine speed 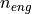 is calculated
for each gear, which would result from the current velocity
is calculated
for each gear, which would result from the current velocity 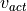 ,
as well as the maximum engine torque
,
as well as the maximum engine torque  and the engine drag
torque
and the engine drag
torque 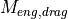 resulting from these engine speeds. Violating the
minimum engine speed
resulting from these engine speeds. Violating the
minimum engine speed 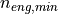 and the maximum engine speed
and the maximum engine speed  is not considered in this step (resulting engine speeds are written as they result
from the powertrain calculation and the engine torques are set to the lower or
upper limits of the characteristic curves respectively, if the engine speed
range is violated).
is not considered in this step (resulting engine speeds are written as they result
from the powertrain calculation and the engine torques are set to the lower or
upper limits of the characteristic curves respectively, if the engine speed
range is violated).
The results above are further processed in a second for-loop over all gears. The following aspects are checked to determine, if a gear fits the current required state:
Is the resulting engine speed
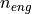 within the range of
within the range of 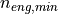 and
and  ?
?Is the resulting engine torque
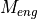 to produce the required
acceleration
to produce the required
acceleration 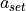 within the range of
within the range of 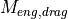 and
and  ?
?
The lowest gear that fits these criterions sets a Boolean foundGear true and the
results (gear number and resulting engine speed 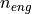 ) are written in
the result vector. This is done for all further gears, until a gear does not fit
the requirements anymore. This initiates the return of the last sufficient gear
and its resulting engine speed
) are written in
the result vector. This is done for all further gears, until a gear does not fit
the requirements anymore. This initiates the return of the last sufficient gear
and its resulting engine speed 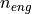 . A short example should
illustrate this logic:
. A short example should
illustrate this logic:
The 2nd gear activates the Boolean foundGear, because
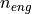 does
not exceed
does
not exceed  anymore
anymoreThe 4th gear activates the return of the results, because the required engine torque
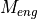 would exceed the maximum possible engine torque
would exceed the maximum possible engine torque  at the corresponding engine speed
at the corresponding engine speed 
The algorithm chooses the 3rd gear as optimum and returns it and its corresponding engine speed
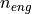
This logic therefore guarantees, that always the highest possible gear is chosen by the driver.
Transient behaviour application
The application of the transient behaviour is modelled as a discrete first order
controller with an amplification equal one. The input signal is the static pedal
position  from the inverted longitudinal dynamics model
and the output signal is the real pedal position
from the inverted longitudinal dynamics model
and the output signal is the real pedal position 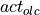 of the
open-loop acceleration controller. A discrete first order controller calculates
the value of the output signal for the current time step
of the
open-loop acceleration controller. A discrete first order controller calculates
the value of the output signal for the current time step 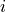 , depending on the
current value of the input signal and the value of the output signal from the
last time step
, depending on the
current value of the input signal and the value of the output signal from the
last time step 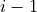 by using two factors
by using two factors 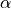 and
and 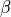 .
Its transfer function is described as:
.
Its transfer function is described as:
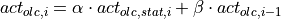
The more common form of a first order controller is the continuous transfer
function, including a time constant 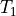 and the time derivative
and the time derivative
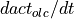 of the output signal (amplification is also neglected):
of the output signal (amplification is also neglected):
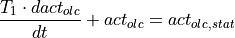
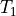 expresses, how long the output signal needs to exceed 63 % of the
input signal. The change
expresses, how long the output signal needs to exceed 63 % of the
input signal. The change 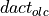 of the output signal can also be
written in a discrete form and the change dt of time can be interpreted as the
step size of the discrete simulation. The ratio of the step size towards the
time constant
of the output signal can also be
written in a discrete form and the change dt of time can be interpreted as the
step size of the discrete simulation. The ratio of the step size towards the
time constant 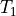 is furthermore substituted with
is furthermore substituted with 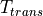 ,
which is dimensionless:
,
which is dimensionless:
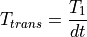
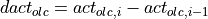
The continuous form can therefore be transformed to match the discrete form above:
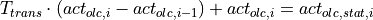
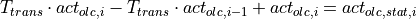
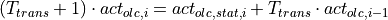
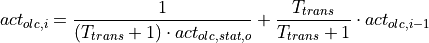
A comparison of coefficients between the two transfer functions result in the
following equations for the factors 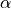 and
and 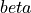 :
:
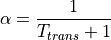
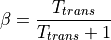
The behaviour is parameterized through 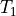 to make it independent
from the simulation step size. For normal situations,
to make it independent
from the simulation step size. For normal situations, 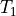 is set to
0.12 s. If the controller detects a major brake manoeuvre,
is set to
0.12 s. If the controller detects a major brake manoeuvre, 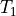 is set
to 0.08 s. A major brake manoeuvre is declared by a desired brake pedal position
greater or equal to 60 % of the maximum possible pedal actuation way.
The calculations above are done in the function ApplyFirstOrderTransientBehaviour
of the sub-module ALongitudinalDataProvider. It is applied to the
inverted longitudinal dynamics model
in the function ControllerPedalPosition of AlgorithmLongitudinalDriver.
is set
to 0.08 s. A major brake manoeuvre is declared by a desired brake pedal position
greater or equal to 60 % of the maximum possible pedal actuation way.
The calculations above are done in the function ApplyFirstOrderTransientBehaviour
of the sub-module ALongitudinalDataProvider. It is applied to the
inverted longitudinal dynamics model
in the function ControllerPedalPosition of AlgorithmLongitudinalDriver.
Compensatory control on stabilization level
The velocity controller is designed as a simple proportional controller. The
general transfer function of a P-controller with the input signal velocity error
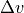 and the output signal pedal position
and the output signal pedal position 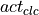 is described as:
is described as:
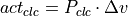
The controller amplification  is therefore described as the ratio
between input signal and output signal:
is therefore described as the ratio
between input signal and output signal:
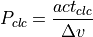
The controller amplification  therefore expresses how many
percent of accelerator or brake pedal position are generated by 1 m/s velocity
error.
therefore expresses how many
percent of accelerator or brake pedal position are generated by 1 m/s velocity
error.  is currently a constant with a value of 0.5 s/m, which
was empirically determined in the Ph.D. thesis of Marcus Mai, Dresden University
of Technology. A dead zone of
is currently a constant with a value of 0.5 s/m, which
was empirically determined in the Ph.D. thesis of Marcus Mai, Dresden University
of Technology. A dead zone of 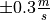 for
for 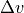 is also implemented
within the controller, which has to be exceeded for the controller even doing
anything.
is also implemented
within the controller, which has to be exceeded for the controller even doing
anything.
As Fig. 52 illustrates, the calculation of 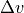 is done by subtracting
the actual velocity
is done by subtracting
the actual velocity 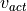 of the vehicle from the desired velocity
of the vehicle from the desired velocity
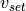 by the driver behaviour model, which is the desired acceleration
by the driver behaviour model, which is the desired acceleration
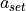 integrated over time:
integrated over time:
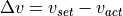
As openPASS is a time discrete simulation platform, integration of values over
time must also be done in incremental steps. In relation to 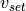 ,
this means which value the velocity in the current time step i should have,
if
,
this means which value the velocity in the current time step i should have,
if 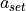 from the last time step
from the last time step 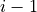 would have been applied
properly to the actual velocity
would have been applied
properly to the actual velocity 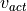 in this last time step,
considering the step size dt:
in this last time step,
considering the step size dt:
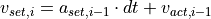
The calculations above are done in the function ClosedLoopController of the sub-module ALongitudinalDataProvider. It is applied to the open-loop controller in the function ControllerPedalPosition of AlgorithmLongitudinalDriver.
Application of the pedal change time
The application of the pedal change time is done by the function RegardPedalChange,
which calls further sub-functions. It checks, if a sign change in the controller
output act occurs and counter checks it towards already ongoing pedal changes.
If a pedal change have to be applied, a pedal change time is sampled from a
lognormal distribution, which is defined by a minimum value, a mean value and a
standard distribution. These parameters are received from the module
ParametersAgent. The sampling of a
new value from this distribution is done for each pedal change to consider
intra-individual differences of the driver. Over the next time steps, the time
since the beginning of the pedal change is summed up, until the pedal change
time is met. In this time frame, no actuation of any pedal is possible and the
output values 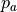 and
and 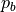 are set to zero. After the
completion of the pedal change, the actuations from the controllers are further
processed and split up into the output signals.
are set to zero. After the
completion of the pedal change, the actuations from the controllers are further
processed and split up into the output signals.