Module 2.5: Computing state spaces
We discussed the concept of a state space of a discrete event system before, in Modules 1.2 and 1.3. You learned that a state consists of a current location for each automaton, and a current value for each variable. And the state space consists of all reachable states and the transitions between them.
We have since discussed interaction of automata, through synchronization on shared events, as well as reading shared variables. It is therefore time to revisit the concept of state space, and learn how to compute it.
First, we will compute the state space for a model without variables. Then, we consider the more general case of computing the state space of a model with variables.
Without variables
Rather than modeling a large system using a single automaton, you learned how to model it using multiple automata that synchronize. Of course, the behavior of the single automaton and the multiple synchronizing automata should then be the same, if they model the same system. That is, they should have the same state space.
A model with multiple synchronizing automata can be transformed to a single automaton, with the same behavior. Each location of the resulting automaton then represents a state of the state space, and thus a current location of each automaton, and a current value of each variable.
Remember that an event that is not shared between automata, can occur when the one automaton that uses it can take an edge for the event. But, for events that are shared between two or more automata, they can only perform the event together, as they must synchronize and take their edges at the same time.
To compute the state space, we start by making an empty automaton to represent the computed state space. We then identify the initial state, and we make an initial location for it in the empty automaton. We then see what transitions are possible for the different events of the system, and add edges for them. By taking the transitions, we likely reach new states, and we add new locations for them. We then explore the transitions from these new states and add edges for them, and we also add new locations for the new states that we reach, and so on. We mark every location as marked, if the corresponding state is marked.
Let's see how this works, by means of an example:


We have two automata, and both have two locations.
The initial state consists of the first automaton being in its location L1, and the second automaton in its location R1.
We can represent this as (L1, R1).
We make a new automaton to represent the state space, and a location for this initial state.
Location R1 is a marked location, but location L1 is not, so the initial state is not marked.
We thus do not mark the initial location of the state space automaton.
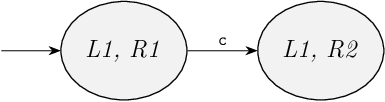
The following figure shows the state space we have constructed so far:

The example has three events: a, b and c.
We check whether transitions are possible for these events, from the initial state.
We start with event a.
Neither location L1, nor location R1 has an outgoing edge for the event, so no transitions for event a is possible in the initial state.
We then proceed to event b.
The first automaton has an outgoing edge for the event in location L1.
But, the second automaton also uses the event, and has no outgoing edge for the event, from its location R1.
In the initial state, it is thus not possible for the two automata to synchronize for the event, and therefore no transitions are possible for b in the initial state.
We then proceed to event c.
The second automaton has an outgoing edge for it in location R1.
The first automaton does not, but it does not synchronize on the event, the second automaton can perform a transitions for the event by itself.
This is thus the only transition possible in the initial state.
By taking this transition, the first automaton remains in its L1 location, as it does not participate.
And the second automaton goes from its R1 location to its R2 location.
We thereby reach a new state (L1, R2), and add a new location for it in the state space automaton.
Location L1 is not marked, and neither is location R2, so the new state is not marked.
We add an edge to connect the two locations, as the two states of the state space are connected by the transition.
We have considered all transitions from the initial state, and thus all states that can be reached from it by a single transition.
The following figure shows the state space we have constructed so far:
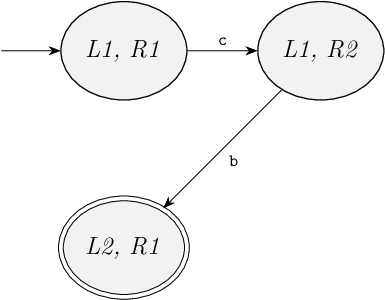
We proceed to the (L1, R2) state, to see what transitions are possible from that state.
Here, transitions for events a and c are not possible.
A transition for event b is possible, since both locations L1 and R2 have outgoing edges for the event.
The two automata synchronize and take their edges at the same time, resulting in a single transition for event b.
This takes us to yet another new state, namely (L2, R1).
We add a new location for this state, and also add an edge for the transition.
Since both L2 and R1 are marked, the new state is a marked state, and we thus mark the new location of the state space automaton.
The following figure shows the state space we have constructed so far:
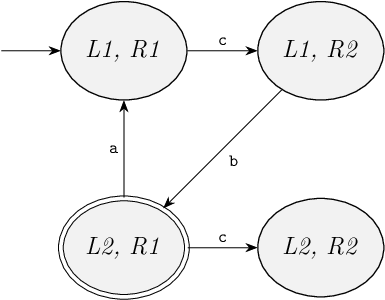
We then consider the transitions possible from state (L2, R1).
A transition for event a is possible in the first automaton.
The second automaton does not participate.
The transition takes us to state (L1, R1), which is the initial state.
Since no new state is reached, we don't add a new location.
We do add an edge for the new transition, between the locations representing states (L2, R1) and (L1, R1).
No transition is possible for event b, as neither automaton has an outgoing edge for it in its current location.
A transition is possible for event c, in which only the second automaton participates.
We reach a new state, (L2, R2), for which we add a new unmarked location to the state space automaton.
We also add an edge for the new transition.
The following figure shows the state space we have constructed so far:
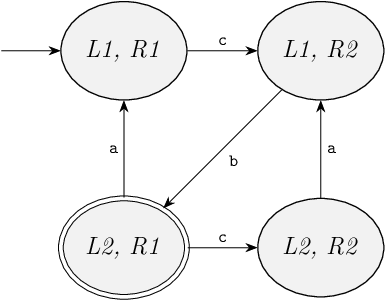
We then consider the transitions possible from state (L2, R2).
A transition is possible for event a, in which only the first automaton participates.
This takes us to state (L1, R2) that we have seen before.
We add an edge for the new transition, but since no new state is reached, we don't add a new location.
No transitions are possible for events b and c.
We have explored all transitions that are possible from all of the reachable states, and have thus computed the full state space.
The following figure shows the complete state space:
The model with the computed state space automaton has the same behavior as the original model with the two synchronizing automata. The same sequences of events are possible in both models. And if a part of such a sequence is executed on both models, they each reach a certain state, and these two states that are either both marked or both unmarked.
With variables
Now let's consider the computation of a state space for a model with variables. The procedure is mostly the same. We start again by determining the initial state. This time we need to consider not only the initial locations of the automata, but also the initial values of the variables. The initial state is a marked state if initial locations of the automata are also marked locations, and the initial values of the variables are marked values.
We then consider possible transitions from the initial state. We therefore consider again each event separately. We check whether each automaton that synchronizes over the event has an outgoing edge from its current location. But, additionally, we consider whether the guards of the edges are enabled by evaluating them using the current values of the variables. We see which new states we reach by taking the transitions. For this, we consider not only the new locations that are reached by the edges of the automata, but also the new values that the variables get by executing the updates of the edges.
As for models without variables, we keep exploring possible transitions from new states that we reach, and thereby we reach either new states or states that we had already reached before. Once no more new states are reached, we have computed the full state space.
Quiz
(L1, R1), (L1, R2), (L2, R1) and (L2, R2).
Is it always the case that the states of the state space are all possible combinations of the locations of the separate automata for which the product is computed (assuming no variables, and that all locations are locally reachable in each automaton)?
So, if a model has 3 automata with 3 locations each, the state space has 33 = 27 locations?`,
answers: [
"Yes, this is indeed always the case, per definition.",
"This depends on whether the model contains non-deterministic automata.",
"No, some states may not be reachable because shared events must synchronize."
],
correctAnswer: '3'
},
{
type: 'single-choice',
question: `
A model consists of 3 automata with respectively 2, 3 and 4 locations.
Within each automaton, all locations are reachable.
Each event is used by only one automaton.
How many locations does the state space have?`,
answers: [
"This can not be determined without more information.",
"29, because 22 + 32 + 42 = 29.",
"24, because 2 * 3 * 4 = 24."
],
correctAnswer: '3'
},
{
type: 'single-choice',
question: "Can the behavior of the state space that is computed be different than the behavior of the model from which it is computed?",
answers: [
"Yes.",
"No.",
"It depends."
],
correctAnswer: '2'
},
{
type: 'multiple-choice',
question: `
Which of the statements is true about the following CIF model (as a whole, not per automaton)?
event a, b, c;
automaton aut1:
location x:
initial;
marked;
edge a goto y;
location y:
edge b goto x;
end
automaton aut2:
location x:
initial;
marked;
edge b goto y;
location y:
edge c goto x;
end
`,
answers: [
"It has a deadlock state.",
"It has no deadlock state.",
"It has a blocking state.",
"It is non-blocking.",
"It has a livelock state.",
"It has no livelock state.",
],
correctAnswer: '2, 4, 6'
},
{
type: 'multiple-choice',
question: `
Which of the statements is true about the following CIF model (as a whole, not per automaton)?
event a, b;
automaton aut1:
location x:
initial;
marked;
edge a goto y;
location y:
edge b goto x;
end
automaton aut2:
location x:
initial;
edge a goto y;
location y:
marked;
edge b goto x;
end
`,
answers: [
"It has a deadlock state.",
"It has no deadlock state.",
"It has a blocking state.",
"It is non-blocking.",
"It has a livelock state.",
"It has no livelock state.",
],
correctAnswer: '2, 3, 5'
},
{
type: 'multiple-choice',
question: `
Which of the statements is true about the following CIF model (as a whole, not per automaton)?
event a, b;
automaton aut1:
location x:
initial;
marked;
edge a goto y;
location y:
edge b goto x;
end
automaton aut2:
location x:
initial;
marked;
edge b goto y;
location y:
edge a goto x;
end
`,
answers: [
"It has a deadlock state.",
"It has no deadlock state.",
"It has a blocking state.",
"It is non-blocking.",
"It has a livelock state.",
"It has no livelock state.",
],
correctAnswer: '1, 4, 6'
},
{
type: 'multiple-choice',
question: `
Which of the statements is true about the following CIF model (as a whole, not per automaton)?
event a, b, c;
automaton aut1:
location x:
initial;
marked;
edge a goto y;
location y:
edge b goto x;
end
automaton aut2:
location x:
initial;
edge b goto y;
location y:
marked;
edge c goto x;
end
`,
answers: [
"It has a deadlock state.",
"It has no deadlock state.",
"It has a blocking state.",
"It is non-blocking.",
"It has a livelock state.",
"It has no livelock state.",
],
correctAnswer: '2, 4, 6'
},
{
type: 'single-choice',
question: `
How many states does the state space of the following CIF model have?
event a, b, c;
automaton aut1:
location x:
initial;
marked;
edge a goto y;
location y:
edge b goto x;
end
automaton aut2:
location x:
initial;
edge b goto y;
location y:
marked;
edge c goto x;
end
`,
answers: [
"Zero.",
"One.",
"Two.",
"Three.",
"Four.",
"Five."
],
correctAnswer: '5'
},
{
type: 'single-choice',
question: `
How many states does the state space of the following CIF model have?
event a, b, c;
automaton aut1:
disc int v = 0;
location x:
initial;
marked;
edge a when v < 3 and v = aut2.v do v := v + 1 goto y;
location y:
edge b goto x;
end
automaton aut2:
disc int v = 0;
location x:
initial;
edge b goto y;
location y:
marked;
edge c do v := v + 1 goto x;
end
`,
answers: [
"Zero.",
"One.",
"Two.",
"Three.",
"Four.",
"Five.",
"Six.",
"Seven.",
"Eight.",
"Nine.",
"Ten.",
"Eleven.",
"Twelve.",
"Infinitely many."
],
correctAnswer: '11'
},
{
type: 'single-choice',
question: `
How many states does the state space of the following CIF model have?
event a, b, c;
automaton aut1:
disc int v = 0;
location x:
initial;
marked;
edge a when v < 3 do v := v + 1 goto y;
location y:
edge b when v = aut2.v goto x;
end
automaton aut2:
disc int v = 0;
location x:
initial;
edge b goto y;
location y:
marked;
edge c do v := v + 1 goto x;
end
`,
answers: [
"Zero.",
"One.",
"Two.",
"Three.",
"Four.",
"Five.",
"Six.",
"Seven.",
"Eight.",
"Nine.",
"Ten.",
"Eleven.",
"Twelve.",
"Infinitely many."
],
correctAnswer: '3'
}
]