Module 3.2: Synthesis guarantees
Supervisory controller synthesis can be used to automatically synthesize a supervisor model from a model of the uncontrolled system and some additional requirements. The theory behind supervisory controller synthesis gives us several guarantees about the synthesized supervisor, namely that the controlled system (the plant combined with the supervisor) satisfies four properties. And we may refer to such a synthesized supervisor controlling the plant as also satisfying these properties. The four properties are: safety, controllability, non-blockingness and maximal permissiveness. The safety guarantee means that the controlled system is safe, in that it adheres to all user-provided requirements, which is covered in Module 4. Here, we will look at the controllability, non-blockingness and maximal-permissiveness guarantees in a bit more detail.
Controllability
In the supervisory control loop a supervisor restricts certain events of the plant from occurring in a controlled system. Controllability is about which events a supervisor can control, and which it can't. The guarantee of controllability then states that, compared to the plant behavior, a synthesized supervisor will never restrict the occurrence of events that it can't control.
To make it clear which events a supervisor can control, and which it can't, there are two kinds of events in supervisory control: controllable events and uncontrollable events. A supervisory controller may restrict when controllable events are allowed to occur, but may not restrict the occurrence of uncontrollable events. All events of a system are therefore labeled as being either controllable or uncontrollable.
As a simple example, consider a machine with a button and a motor. Pushing the button starts the motor, and releasing the button stops the motor. This system could be modeled as follows, with the top two automata being the plant and the bottom automaton being the supervisor:
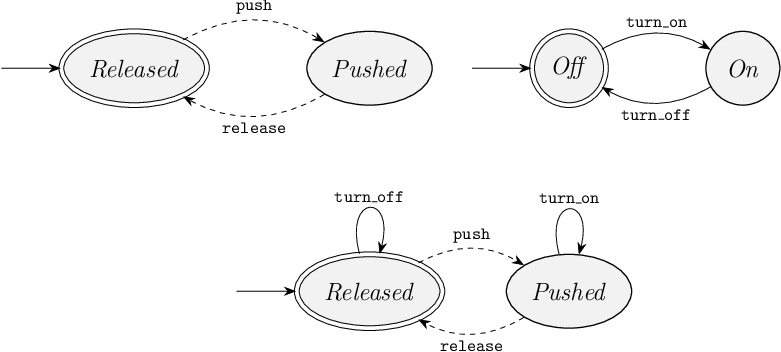
The top-left automaton models the button. It is a sensor that indicates whether the operator is pushing the button or not. Initially, the button is Released. When the operator pushes the button, it is becomes Pushed. When the operator releases the button, it becomes Released again.
The top-right automaton models the motor. Initially, the motor is Off. Once it is turned on, it becomes On. Once it is turned off, it becomes Off.
The bottom automaton models the interactions between the button and the motor. It determines, based on the state of the button, what may happen with the motor. The automaton is a copy of the button automaton, with some extra self-loop edges. In the location where the button is Pushed, the motor may be turned on. In the location where the button is Release, the motor may be turned off.
Through synchronization, all three automata together model the correct operation of the system. For instance, without the bottom automaton, the motor can be turned on and off at any time, without any relation to the button. And even though the top-right automaton allows a motor to be turned on repeatedly, the bottom automaton indicates this is not possible, as a motor can only alternatingly be turned on and off. The behavior of the top-left automaton is contained in the behavior of the bottom automaton, and could be removed without changing the behavior of this system. We will see later in the course why it is still good to model each part of a system separately, and only then restrict their combined behavior.
You may have already observed that some of the edges are depicted as solid arrows, while others are depicted as dashed arrows. The dashed arrows are edges with uncontrollable events. In this case, the button events are uncontrollable events. The operator can always push or release the button. The supervisor can't prevent this. The supervisor must never restrict these events from occurring, as it can't physically prevent the operator from pushing or releasing the button.
The motor however, is fully under the control of the supervisor. The supervisor can and should decide when it is allowed to allow turn it on or off. The events to turn the motor on or off are therefore controllable events, indicated by solid arrows.
While it is not done in this simple example, a supervisor could for instance disable turning on the motor if somebody is near the machine, to prevent injuries. It could do so, even if the operator pushes the button. This would of course require adding an extra sensor to the system, to detect a person approaching the machine.
In general, for supervisory controllers that interact directly with hardware components, actuators are generally modeled as controllable events, while sensors are generally modeled as uncontrollable events. For higher-level supervisory controllers that control sub-systems, the signals the controller gets from the sub-systems are generally modeled as uncontrollable events, and the commands it gives to the sub-systems are generally modeled as controllable events. A supervisor may disable controllable events, but may never disable uncontrollable events. It is up to the modeler to decide for each event whether it is controllable or uncontrollable.
And that brings us back to the guarantee of controllability. A synthesized supervisor is guaranteed to be controllable, meaning that it in the controlled system it only disables controllable events, but never uncontrollable ones. A supervisor is thus free to enable or disable controllable events whenever it deems appropriate. But, for any state that is reachable in the controlled system, if in the same state in the uncontrolled system an uncontrollable event is possible, then the event must also be possible in the controlled system.
Modeling controllable and uncontrollable events in CIF
When modeling for supervisory controller synthesis, the events in a CIF model need be distinguished as being controllable or uncontrollable.
The event keyword can be replaced by controllable to indicate that the declared events are controllable events, or by uncontrollable to indicate that they are uncontrollable events.
Instead of controllable it is also allowed to write controllable event, and similarly for uncontrollable event instead of uncontrollable.
In CIF, it is customary to give controllable events a name that starts with c_ and uncontrollable events a name that starts with u_.
If you follow this convention, then the controllable and uncontrollable events get a different color, making it easier to distinguish them.
For instance, some controllable and uncontrollable events could be declared in CIF as follows:
controllable c_start, c_stop;
uncontrollable u_pushed, u_released;
Quiz
breakdown.",
"Event call_mechanic.",
"Event repair_finished.",
"Event start_repair."
],
correctAnswer: '1'
},
{
type: 'single-choice',
question: `
Consider a system with a plant automaton and a supervisor automaton.
The initial location of the plant has two outgoing edges, one with controllable event a and one with uncontrollable event b.
The supervisor's initial location has only one outgoing edge with event a, leading to the second location.
The second location of the supervisor has two outgoing edges with events a and b.
Is this controlled system controllable?
Hint: Try to draw the situation.
`,
answers: [
"Yes, because the supervisor controls the plant by synchronizing with it.",
"No, because when the automata are in their initial locations, the supervisor has no edge for b, meaning it disables an uncontrolled event that is possible in the plant.",
"Yes, because the alphabets of both automata are the same, which through synchronized events sometimes leads to events getting disabled, without affecting controllability."
],
correctAnswer: '2'
},
{
type: 'single-choice',
question: `
Consider an alternative button/motor system, where a first push of the button turns on the motor, a second push turns it off, a third push turns it on again, and so on.
The following automata can be used to model this.
If we consider the top two automata as the plant and the bottom one as the supervisor, then this system is controllable.
But, we may wonder whether the two curved edges with event push in the bottom automaton are really needed.
Would the system still be controllable if the two edges would be removed?
Hint: Consider the state spaces of the uncontrolled system and controlled system, their corresponding states, and which uncontrollable events are enabled in corresponding states.
`,
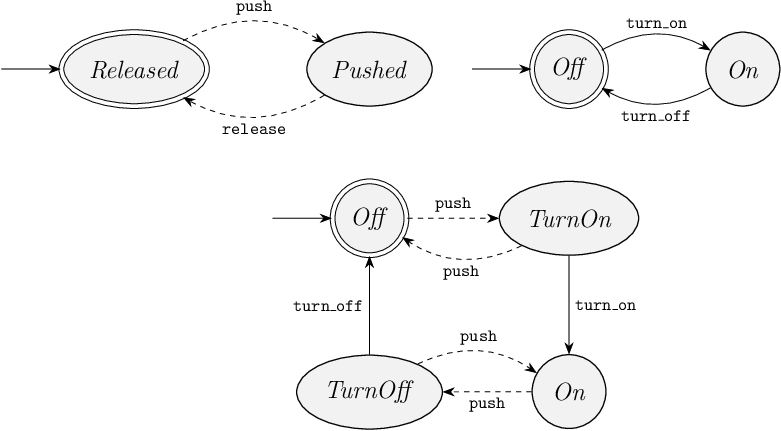answers: [
"Yes, then the system is still controllable, because the supervisor still has two edges for the push event and that event is thus also still in the alphabet of the supervisor.",
"Yes, then the system is still controllable, since the button plant specifies that between two pushes of the button always a release must happen, and therefore the supervisor does not disable any uncontrollable events of the plant.",
"No, then the system is not controllable anymore, as the supervisor disables the push event in states where it is possible in the plant.",
"No, then the system is not controllable anymore, because the modeler added these edges for a reason."
],
correctAnswer: '3'
}
]
Non-blockingness
In Module 2, you learned about blocking states. Recall that a state is blocking if it is not marked and it is also not possible to reach a marked state from it by taking one or more transitions. Marked states are stable states or safe havens. For instance, for safety reasons, it must always be possible to turn off a machine. And in a production system, if a product enters a system, it must always be able to leave the system again, after having been processed. In general, once the system leaves a marked state, it can be seen as performing some task, and it must complete the task, before going back to a marked state. The system must be able to progress to a stable state, rather than for instance getting stuck.
As another example, think for instance of a car. Before you enter it, it is off and empty, which could be its marked state. Let's say you want to go for a short trip. You enter the car and you start it. Only once you've reached your destination, do you want to turn off your car and exit it. The car is then off and empty again, and back in its marked state.
It is thus important that in a controlled system all reachable states are non-blocking. They are thus either themselves marked, or from each of them it is possible to reach a marked state. When a synthesized supervisor is combined with the plant, the resulting controlled system is guaranteed to be non-blocking. In other words, in a controlled system with a synthesized supervisor no reachable state is blocking. It is up to the modeler to ensure proper marked states are defined, such that the stable states are appropriate for the system.
Quiz
A and B.
Location A is a deadlock location, is not initial and is not marked.
Location B has one outgoing edge leading to location A.
Are A and B blocking?
`,
answers: [
"A is blocking because it has deadlock and is not marked. B is non-blocking because further behavior is possible (it has an outgoing edge).",
"You cannot know whether A and B are blocking, because you need to know the rest of the automaton.",
"A and B are both blocking: A is blocking because it has deadlock and is not marked, and B is then also blocking because its only outgoing edge leads to a blocking location.",
"A is blocking because it has deadlock and is not marked. For B it depends on whether it is a marked location, which is not stated in the question."
],
correctAnswer: '4'
},
{
type: 'single-choice',
question: `
Consider again the car/motor example from earlier in this sub-module, where a button push turns on the motor and releasing the button turns it off.
Is this system non-blocking?
`,
answers: [
"Yes.",
"No.",
"It depends."
],
correctAnswer: '1'
},
{
type: 'single-choice',
question: `
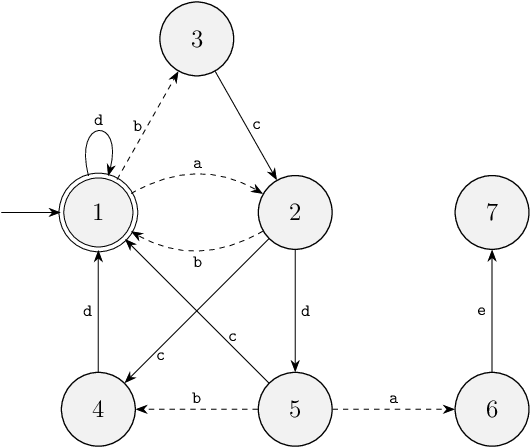
Consider the following automaton.
Is this a proper non-blocking plant, that does not need a supervisor to restrict any of its behavior to make it non-blocking?
`,
answers: [
"Yes, since the plant doesn't have any blocking behavior.",
"No, since locations 6 and 7 are blocking.",
"This can't be determined as it is unclear what the system represents."
],
correctAnswer: '2'
},
{
type: 'single-choice',
question: `
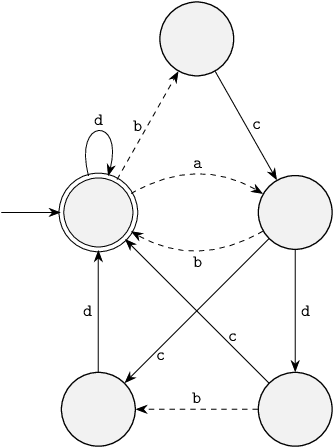
If we add the following supervisor to the plant of the previous question, is the controlled system then controllable and non-blocking?
`,
answers: [
"Yes, since it removes the blocking behavior by disabling event a in location 5.",
"No, since it disables uncontrollable event a, which means it is not controllable.",
"This can't be determined, as the system that the automaton represents is not known."
],
correctAnswer: '2'
}
]
Controllability revisited
In the quiz just now, you saw that it is not always sufficient for a supervisor to simply prevent reaching non-blocking states.
The supervisor prevents reaching locations 6 and 7 of the plant.
But, it does so by disabling event a in location 5.
Since in the controlled system this location is reachable, and the plant does allow event a then, the controlled system is not controllable.
So, what can be done here?
Preventing the system from reaching locations 6 and 7 of the plant is required to satisfy non-blockingness.
This makes location 5 a so-called bad location.
In general, non-blocking states are bad, because they are not marked and from them no marked state can be reached.
But, states from which a transition for an uncontrollable event leads to a bad state, are in turn also bad.
This means that location 5 is a bad location in this case.
In a way, the badness of location 6 is pushed backwards through the dashed arrow to location 5.
Since there are no dashed arrows to location 5, no further backwards propagation is needed.
To ensure controllability, supervisor synthesis computes all this automatically. It prevents reaching blocking states, but also prevents reaching any states from where via uncontrollable events such states can be reached. It thus prevents all such bad states from being reached.
Maximal permissiveness
The final guarantee of synthesis that we'll look at here, is maximal permissiveness. Consider the following three supervisors, that remove all bad states from the example system that we just looked at:
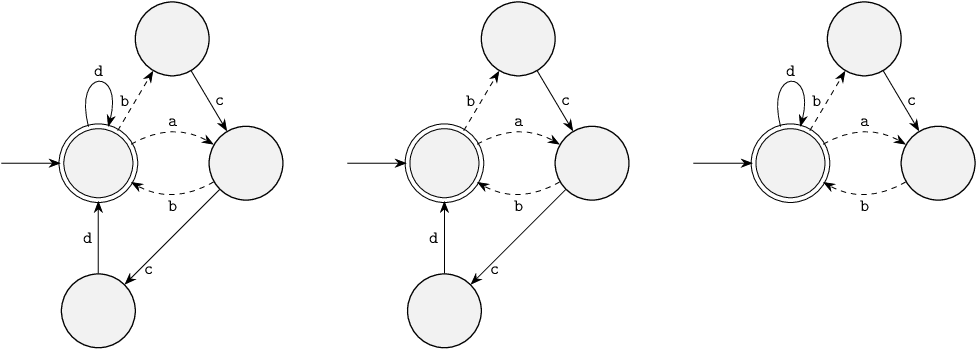
These three supervisors each ensure that the controlled system is both non-blocking and controllable. Still, they don't all allow the same behavior in the controlled system. In fact, it is often the case that multiple supervisors exist that make the controlled system non-blocking and controllable.
This poses the question which of the multiple possible supervisors we prefer. There could be many reasons for preferring one supervisor over another. The reasons may include aspects that are not modeled, such as performance, cost, energy consumption or wear and tear. Supervisor synthesis opts to not put any restrictions on the system, unless they are required to satisfy one of its guarantees. For instance, it will remove all states that are bad due to being blocking or violating the controllability guarantee. The maximal-permissiveness guarantee means that synthesized supervisors only restrict the behavior of a system as much is needed to satisfy the other guarantees. They do not unnecessarily restrict any more behavior, and are thus minimally restrictive. The guarantee is therefore also called minimal-restrictiveness.
After synthesis, other means can then be used to further restrict the behavior. For instance, consider a system where two machines process products. A supervisor may decide to always use the first machine, always use the second machine, or to use both machines. Since a synthesized supervisor is maximally permissive, it allows all these options. To prevent not using one of the machines, and also prevent the one machine that is used from quickly wearing out, one could alternate products between the machines. Depending on the criteria, it may be possible to include these decisions already during synthesis, or the choice can be made afterwards using different techniques. Such other techniques are outside the scope of this course.
Let's go back to the three supervisors in the figure above.
The middle and right supervisors lacks some behavior that the left supervisor has.
For instance, the right supervisor lacks the bottom location and its incoming and outgoing edge.
The left supervisor has all the behavior that the middle and right ones have, and more.
This is the maximally-permissive supervisor for the plant of this example.
It is identical to plant, but with bad locations 5, 6 and 7, as well as all their incoming and outgoing edges, removed.
Besides that, nothing else is removed, making this is the maximally-permissive supervisor.
Quiz
d in plant location 1, while the left supervisor does not unnecessarily restrict any behavior of the plant.",
"The left supervisor unnecessarily disables event d in plant location 1, while the middle supervisor does not unnecessarily restrict any behavior of the plant.",
"Maximally permissive simply means maximal in size, and because the left supervisor is bigger than the middle one, the left supervisor is maximally permissive."
],
correctAnswer: '1'
},
{
type: 'multiple-choice',
question: `
Consider again the example used to explain deadlock, from a previous module.
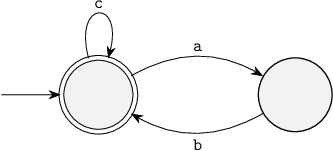
If we consider that automaton the plant model, which statements are then correct about the following supervisor?
`,
answers: [
"It removes non-marked deadlock location 3, making the system non-blocking.",
"It is controllable, since no uncontrollable events are defined at all.",
"It does not restrict any more behavior of the plant than is strictly needed, and is therefore maximally permissive.",
],
correctAnswer: '1, 2, 3'
},
{
type: 'multiple-choice',
question: `
Consider again the example automaton used to explain blocking, from a previous module, where location 2 is marked.
If we consider that automaton the plant model, which statements are then correct about the following supervisor?
`,
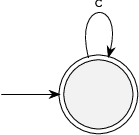answers: [
"It is non-blocking.",
"It is controllable, since no uncontrollable events are defined at all.",
"It does not restrict any more behavior of the plant than is strictly needed, and is therefore maximally permissive.",
],
correctAnswer: '1, 2, 3'
},
{
type: 'single-choice',
question: "Does the plant automaton considered in the previous question need a supervisor?",
answers: [
"Yes, the uncontrolled system always needs a supervisor.",
"No, the automaton is by itself already a proper controlled system."
],
correctAnswer: '2'
}
]
Properties of the supervisor and the controlled system
If a controlled system consisting of a plant and a supervisor is non-blocking, controllable and maximally permissive, then the supervisor that controls the plant is also non-blocking, controllable and maximally permissive. The inverse is however not always true in regard to non-blockingness. That is, if the plant and supervisor by themselves are both non-blocking, then their combination may be blocking and thus the controlled system is then blocking.
Quiz
`,
answers: [
"The plant is non-blocking.",
"The supervisor is non-blocking.",
"The controlled system is non-blocking.",
],
correctAnswer: '1, 2, 3'
},
{
type: 'multiple-choice',
question: `
Consider the following plant (left) and supervisor (right).
Which of these statements are correct?
`,
answers: [
"The plant is non-blocking.",
"The supervisor is non-blocking.",
"The controlled system is non-blocking.",
],
correctAnswer: '1, 2'
},
{
type: 'multiple-choice',
question: `
Consider the following plant (left) and supervisor (right).
Which of these statements are correct?
`,
answers: [
"The plant is non-blocking.",
"The supervisor is non-blocking.",
"The controlled system is non-blocking.",
],
correctAnswer: '1, 2, 3'
}
]