Module 2.1: Reachability, deadlock, blocking and livelock

Reachability, deadlock, blocking and livelock are important concepts to understand automata, and are essential to later understand how synthesizing a supervisory controller works. We first discuss reachability, then deadlock, and then the related concepts of blocking and livelock.

Reachability

States are reachable if there is a way to get there. Initial state are per definition reachable. Any other state is only reachable if there is a sequence of transitions from the initial state to that state.

A state of a discrete event system consists of a current locations for each automaton and a current value for each discrete variable. An initial state thus consists of an initial location for each automaton, and an initial value for each discrete variable.

A location of an automaton is reachable if there is a way to get to the location from the initial location of that automaton. Initial locations of automata are per definition reachable. Other locations are only reachable if there are edges that can be taken to get those locations, starting from the initial location. A value of a variable is reachable if there is a way to assign that value to the variable, by starting from the initial state and taking edges.

In the figure below, an example automaton is shown. Location 1 is its initial location. It is per definition reachable, and can be reached without taking any edges. Location 2 is reachable, because there is an edge from reachable location 1 to location 2. We can reach location 2 by a transition for event a. Location 1 is also reachable by a sequence of transitions for events a and b. And location 2 is also from the initial state by transitions for events a, b and a. However, to show that a state is reachable, it is sufficient to have one sequence to reach it, and the shortest sequence is then sufficient. Location 3 is not reachable, because there is no such sequence of edges to get to it from location 1.

Unreachable states can't be reached from initial states. They are thus not very useful when modeling a system. Therefore, unreachable locations of automata are typically omitted from models.

Deadlock

A deadlock state is a state where no transitions are possible, and thus no further behavior is possible. Since a discrete event system can transition between states by taking edges, if no more transitions are possible, this means no edges can be taken.

A location is a deadlock location if it has no outgoing edges. Then, per definition, if such a location is the current location of its automaton, the automaton deadlocks. But, an automaton can also deadlock in a location that does have outgoing edges, but where none of the guards of these edges is satisfied. If for instance a location has one edge, with a guard x > 3, but while being in that location x has value 2, then the edge can't be taken, and the automaton is stuck in the location.

The figure below shows an example of an automaton with a deadlock location. All three locations are reachable from the initial location. Location 3 for instance is reachable by taking transitions for events a and c. But once the automaton transitions to location 3, there is no way to leave that location, and thus the automaton is in a deadlock.

Since in a deadlock state no further behavior is possible, such states are of course undesired. A supervisory controller should prevent the system from ending up in such a state, as we will explore further in Module 3.

Blocking and livelock

In Module 1, you learned about marked states. Marked states are stable states, or safe havens. The system should always be able to reach a marked state. For instance, a machine should always be able to reach its idle state. For safety reasons, it is important that a system can always be turned off. And for the correct functioning of a production system, it is important that once a product enters the system, it can also always leave the system again after having been processed.

A system is non-blocking if from every reachable state, it is possible to reach a marked state. All marked states are thus per definition non-blocking. For other states, there must be a sequence of transitions to a marked state. Any state that is reachable, but does not have a sequence of transitions to a marked state, is called a blocking state.

A state is a marked state if all current locations of its automata are marked locations, and all current values of its variables are marked values. Within an automaton, a marked location can be reached if from the current location there are edges that can be taken to get to a location that is marked. A marked value of a variable can be reached by taking an edge that assigns a marked value to the variable. An automaton is blocking if it has at least one blocking location, and a system is blocking if it has at least one blocking automaton.

Below, you see two automata, that only differ by which locations are marked. The first automaton has location 1 as marked location, and thus location 1 is a non-blocking location. Since there is no way to get to location 1 from locations 2 and 3, both these locations are blocking locations. Hence, the automaton and the system are blocking.

The second automaton has location 2 as its marked location, and thus this location is a non-blocking location. From location 1 it is possible to reach location 2 by taking the edge for event c. From location 3 it is also possible to reach location 2 by taking the edge for event b. All the locations, the automaton, and the system are thus non-blocking.

Now look back at the earlier example of the automaton with a deadlock location (location 3). It is in not only a deadlock location, but also a blocking location, as from location 3 it is not possible to reach marked location 1. Often deadlock locations are also blocking locations, but this does not have to be the case. When the deadlock location is also marked, the location is not blocking.

Now look back at the blocking automaton just above (with marked location 1 and blocking locations 2 and 3). Locations 2 and 3 form a loop, and thus always another transition can be taken. The automaton does not deadlock, but while taking further transitions never a marked state can be reached. If progress is still possible by taking transitions, but no marked state can be reached, this is called a livelock.

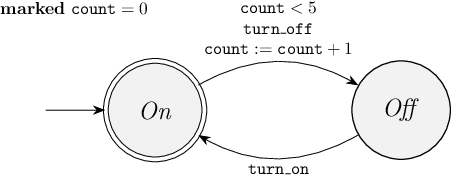
As an example of a blocking state in a model with variables, consider again the example from Module 1.4, of a lamp and a counter that counts the number of times that the lamp is turned off. Through simulation, you observed the behavior of the model. After turning off the lamp five times, and turning on the lamp a final time, no further behavior is possible. The system is then in a deadlock state. Below, the graphical representation of the model is shown. If the On location is the current location, and count has reached value 5, then the guard of the edge with event turn_on is not satisfied. The edge is thus not enabled, and the automaton deadlocks in that state. Location On is marked, but value 5 of variable count is not. Thus, the state is not marked, and since no transitions are possible, it is blocking.

Quiz

                                        
                                            automaton a:
                                                event e1, e2, e3, e4, e5;
                                                disc int v = 4;

                                                location a:
                                                    initial;
                                                    marked;
                                                    edge e1 do v := v + 3 goto b;

                                                location b:
                                                    edge e2 do v := v - 1 goto a;
                                                    edge e3 when v = 8 goto c;
                                                    edge e3 when v = 14 goto c;
                                                    edge e3 when v = 15 goto d;
                                                    edge e4 when v = 15 goto e;
                                                    edge e5 when v = 17 goto f;

                                                location c:
                                                    edge e3;

                                                location d:
                                                    edge e3 when v = 15;

                                                location e:
                                                    edge e3 when v mod 2 = 0;

                                                location f:
                                                    marked;
                                                    edge e3 when v = 15;
                                            end