Module 3.5: Exercises
You will now practice what you have learned in this third module. When modeling, there is generally not one correct answer, as multiple solutions are possible. After you complete an exercise, an example solution is given, together with an explanation.
Exercise 1
Consider the following plant state space.
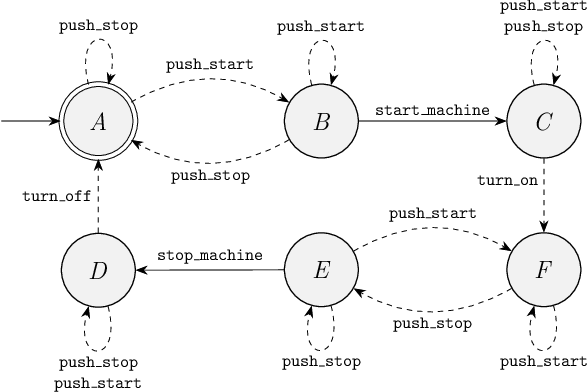
a. Is the following supervisor a proper supervisor for this plant, that ensures the controlled system is controllable, non-blocking and maximally permissive?
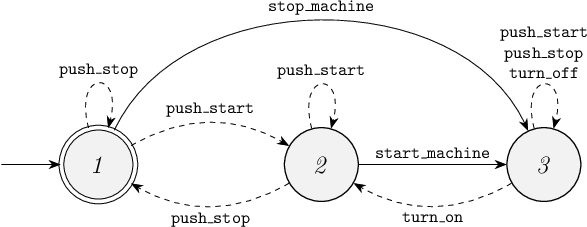
Hint: Compute the controlled system state space to answer this question.
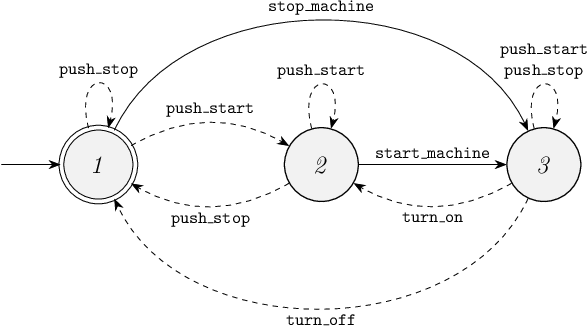
The controlled system state space looks like this:
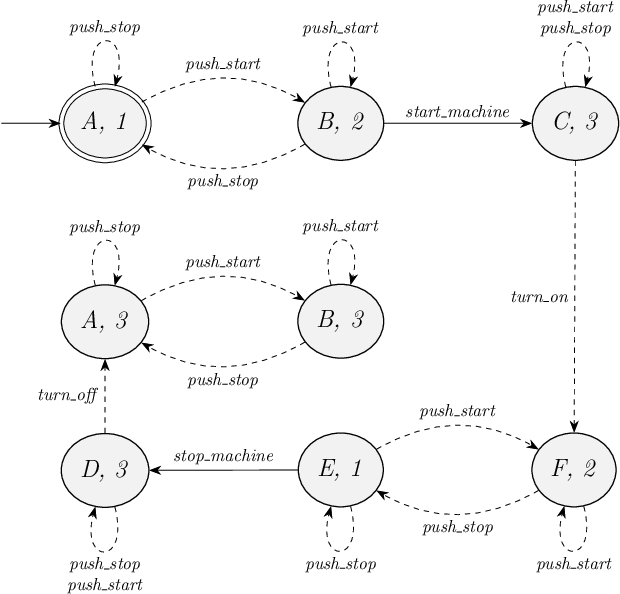
This controlled system is controllable:
-
The plant allows events
push_startandpush_stopin every state, and so does the supervisor. Since they are enabled in every state of the plant and the supervisor, they are also enabled in every state of the controlled system. -
Event
turn_onis only enabled in stateCof the plant. In the single controlled system that matches plant stateC, the event is also enabled. -
And the controlled system similarly does not restrict the occurrence of event
turn_offcompared to the plant.
In fact, the supervisor only restricts event start_machine from occurring in controlled system state (B, 3).
The supervisor automaton itself is non-blocking. However, the controlled system has many blocking states.
The controlled system is not maximally-permissive. To understand why this is the case, consider the following:
- The plant is already non-blocking, so no states need to be removed to ensure the controlled system is non-blocking.
- With no blocking states to remove, also no states need to be removed to ensure controllability.
- In fact, no additional restrictions are needed, and thus the plant itself is its own maximally-permissive supervisor.
With the plant itself being a proper maximally-permissive supervisor, it is easy to see that the given supervisor, and its controlled behavior, are not maximally permissive: the plant can go through many start-stop cycles, while the controlled system can only go through one.
b. What would happen if in location 3 of the supervisor the edge for event push_stop were to be removed?
Would it then be a proper supervisor?
Hint: Compute the new controlled system state space.
The new controlled system state space is depicted below. The red arrows and labels indicate what is removed compared to the previous controlled system state space:
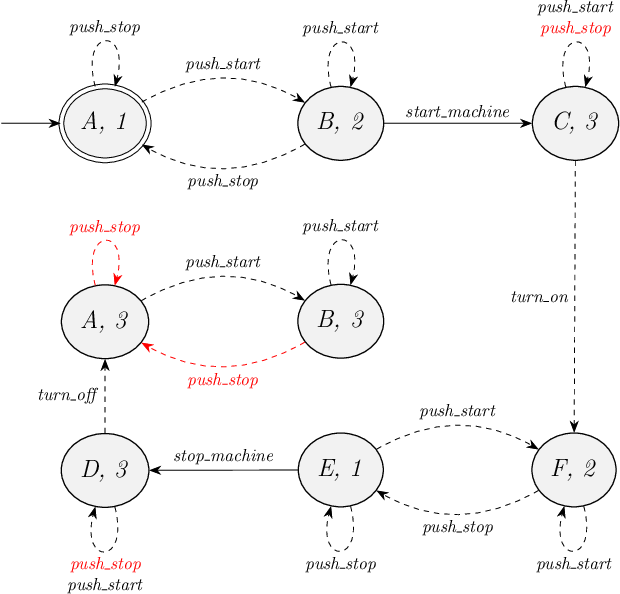
The controlled system is then no longer controllable, since the push_stop event is then disabled in various states of the controlled system, compared to the uncontrolled system (in states with red events on outgoing transitions).
It still has blocking states and thus is still blocking.
It also still restricts the start_machine event and is thus not maximally permissive.
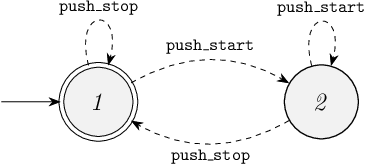
c. Is the following alternative supervisor a proper supervisor for the plant?
d. Apply the synthesis algorithm, using the controlled system state space from the solution to Exercise 1a as plant.
The blocking behavior starts at state (C, 3), so states (C, 3), (F, 2), (E, 1), (D, 3), (A, 3) and (B, 3) are removed.
To make sure state (C, 3) is not reached, event start_machine is disabled in state (B, 2).
Nothing needs to be removed to ensure controllability.
The resulting non-blocking, controllable, maximally-permissive supervisor is:
Note that this supervisor has alphabet push_start, push_stop, turn_on, turn_off, start_machine, stop_machine.
Out of the six events, only two are allowed by the supervisor, and thus in the controlled system.
It never allows uncontrollable events turn_on and turn_off, but this is theoretically OK, since the plant states where these events are enabled can't be reached.
Whether this supervisor makes sense for the actual system we don't know, as we did not explain the system and its purpose.
Generally though, it is a sign of a problem if one ore more events of the system are not enabled in any of the states of the controlled system.
Exercise 2
Synthesize a proper supervisor for the following plant:
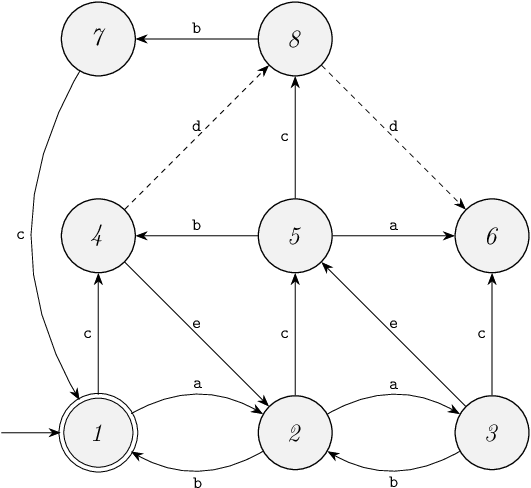
For the first iteration of the synthesis algorithm:
- Blocking state
6is removed. - Since removed state
6has an incoming transition for uncontrollable eventd, state8is removed. - Unreachable state
7is removed. - The
aandctransitions from state5and thectransition from state3are removed.
For the second iteration of the synthesis algorithm:
- There are no blocking states.
- Since removed state
8has an incoming transition for uncontrollable eventd, state4is removed. - There are no unreachable states.
- The
ctransition from state1and thebtransition from state5are removed.
For the third iteration of the synthesis algorithm:
- Blocking state
5is removed. - There are no non-controllable states.
- There are no unreachable states.
- The
ctransition from state2and theetransition from state3are removed.
The fourth iteration of the synthesis algorithm does not lead to any changes.
The resulting supervisor is:
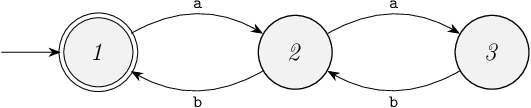
Exercise 3
Consider again the clothing company from a question of the quiz of the previous sub-module, and the answer to that question. Also consider that all of the company's machines are like the machine with a button and a motor, from the example of the controllability synthesis guarantee.
a. Model the clothing company as a plant model in CIF.
The model structure of component definitions/instantiations and group is taken from the quiz question's answer.
The Machine group definition contains the plant automata.
The controllable and uncontrollable have been given names that start with c_ and u_, respectively.
They are then highlighted in different colors.
group def Machine():
plant button:
uncontrollable u_push, u_release;
location Released:
initial;
marked;
edge u_push goto Pushed;
location Pushed:
edge u_release goto Released;
end
plant motor:
controllable c_turn_on, c_turn_off;
location Off:
initial;
marked;
edge c_turn_on goto On;
location On:
edge c_turn_off goto Off;
end
plant interactions:
location Released:
initial;
marked;
edge button.u_push goto Pushed;
edge motor.c_turn_off;
location Pushed:
edge button.u_release goto Released;
edge motor.c_turn_on;
end
end
group def Hall():
machine1: Machine();
machine2: Machine();
machine3: Machine();
machine4: Machine();
end
group def Factory():
hall1: Hall();
hall2: Hall();
end
group def Country():
factory1: Factory();
factory2: Factory();
end
country1: Country();
country2: Country();
country3: Country();
b. Due to regulations, the machines have to be checked regularly. Adapt the CIF model based on the following regulations and constraints.
Regulations:
-
Machines have to be checked after they have been used a certain number of times (we call this the
limit). The regulations differ in each country. In countries 1 it has to be checked after it has been used 6 times. In country 2, it is after 8 times. And in country 3, after 9 times. - An operator of a machine may decide to stall a check until the factory is less busy.
Modeling constraints:
- Parameterize the definitions such that the you only have to enter the
limitat the country instantiations. - Model the checking of a machine by means of a single extra plant automaton, without adapting the existing plant automata.
- Declare the event
check_startto indicate a machine is being checked andcheck_passedto indicate it passed the check. - Make sure the new events are either controllable or uncontrollable.
- While a machine is being checked, it must be off.
An algebraic parameter limit is defined on all group definitions, to allow passing it from each country to each factory, hall and machine.
A single automaton named check is added to the Machine.
It can directly access the limit parameter of the Machine.
The c_check_start and c_check_passed events are modeled as uncontrollable events.
The operator decides when to start checking, and may delay it.
The operator also decides when a machine has passed a check.
A supervisory controller can't prevent the operator from doing so, and thus the events are uncontrollable from the perspective of the supervisor.
The number of times the machine has been used is counted in used.
This number is increased each time the machine is turned off.
To keep track of whether the country-specific limit has been reached, an algebraic variable limit_reached is declared.
Since the operator may delay checking the machine, limit_reached is defined as used >= limit rather than as used = limit.
This allows using the value of the algebraic variable to decide whether an operator may start to check the machine.
The automaton has two locations.
Initially, the system is NotChecking.
Once the operator starts the check, the automaton goes to the Checking location.
The operator may only start the check using the u_check_start event when the limit_reached condition holds.
To make sure the motor is off when the operator starts to check the machine, the u_check_start event is additionally guarded by the motor.Off condition.
To make sure the motor stays off while the operator is checking the machine, the motor.c_turn_on event is only allowed in the Running location, and not in the Checking location.
Since the motor is off in the Checking location, there is no need to allow the motor.c_turn_off event there.
Once the motor has passed the check, the automaton goes back to the NotChecking location.
The used count is then reset.
group def Machine(alg int limit):
plant button:
uncontrollable u_push, u_release;
location Released:
initial;
marked;
edge u_push goto Pushed;
location Pushed:
edge u_release goto Released;
end
plant motor:
controllable c_turn_on, c_turn_off;
location Off:
initial;
marked;
edge c_turn_on goto On;
location On:
edge c_turn_off goto Off;
end
plant interactions:
location Released:
initial;
marked;
edge button.u_push goto Pushed;
edge motor.c_turn_off;
location Pushed:
edge button.u_release goto Released;
edge motor.c_turn_on;
end
plant checking:
uncontrollable u_check_start, u_check_passed;
disc int used = 0;
alg bool limit_reached = used >= limit;
location NotChecking:
initial;
marked;
edge motor.c_turn_off do used := used + 1;
edge motor.c_turn_on;
edge u_check_start when limit_reached and motor.Off goto Checking;
location Checking:
edge u_check_passed do used := 0 goto NotChecking;
end
end
group def Hall(alg int limit):
machine1: Machine(limit);
machine2: Machine(limit);
machine3: Machine(limit);
machine4: Machine(limit);
end
group def Factory(alg int limit):
hall1: Hall(limit);
hall2: Hall(limit);
end
group def Country(alg int limit):
factory1: Factory(limit);
factory2: Factory(limit);
end
country1: Country(6);
country2: Country(8);
country3: Country(9);
c. Adapt the motor automaton in your CIF model such that the interactions automaton can be removed.
The relations automaton ensures the motor can only be turned on while the button is pushed, and can only be turned off while the button is released. This can also be modeled using guards.
plant motor:
controllable c_turn_on, c_turn_off;
location Off:
initial;
marked;
edge c_turn_on when button.Pushed goto On;
location On:
edge c_turn_off when button.Released goto Off;
end
Exercise 4
Consider a system with three machines. For a machine to be started, one of the other machines must be on. Machine 2 can only be started when machine 1 is on, machine 3 can only be started when machine 2 is on, and machine 1 can only be started when machine 3 is on. There is thus a sort of cyclic dependency between the machines.
The machines can be modeled using the following three automata (machine 1 at the top left, machine 2 at the top right, machine 3 at the bottom).
Machine 1 can be started with the s1 event, and it can be turned off using the o1 event.
When machine 1 is On, it enables starting machine 2, by means of the self loop for the s2 event.
The other two machines are modeled similarly.
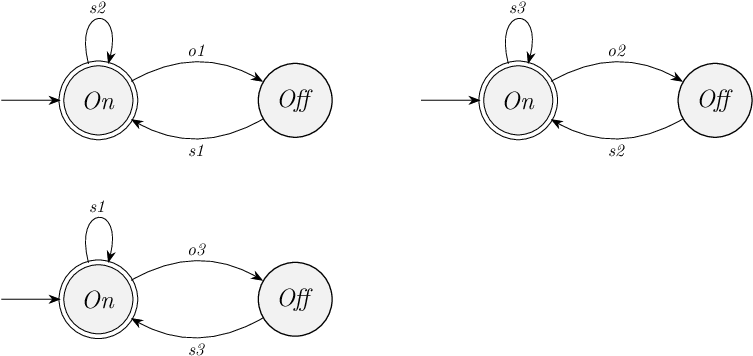
a. Model this system in CIF, compute its state space, and depict it graphically, using CIF tools.
The system can be modeled in CIF as follows:
controllable o1, s1;
controllable o2, s2;
controllable o3, s3;
plant machine1:
location On:
initial;
marked;
edge s2;
edge o1 goto Off;
location Off:
edge s1 goto On;
end
plant machine2:
location On:
initial;
marked;
edge s3;
edge o2 goto Off;
location Off:
edge s2 goto On;
end
plant machine3:
location On:
initial;
marked;
edge s1;
edge o3 goto Off;
location Off:
edge s3 goto On;
end
Note that no c_ prefixes are used, to keep the names of the event as described.
This means the event names are not colored, but remain black.
The state space can use computed using the CIF explorer, and be visualized using the CIF to yEd transformer:
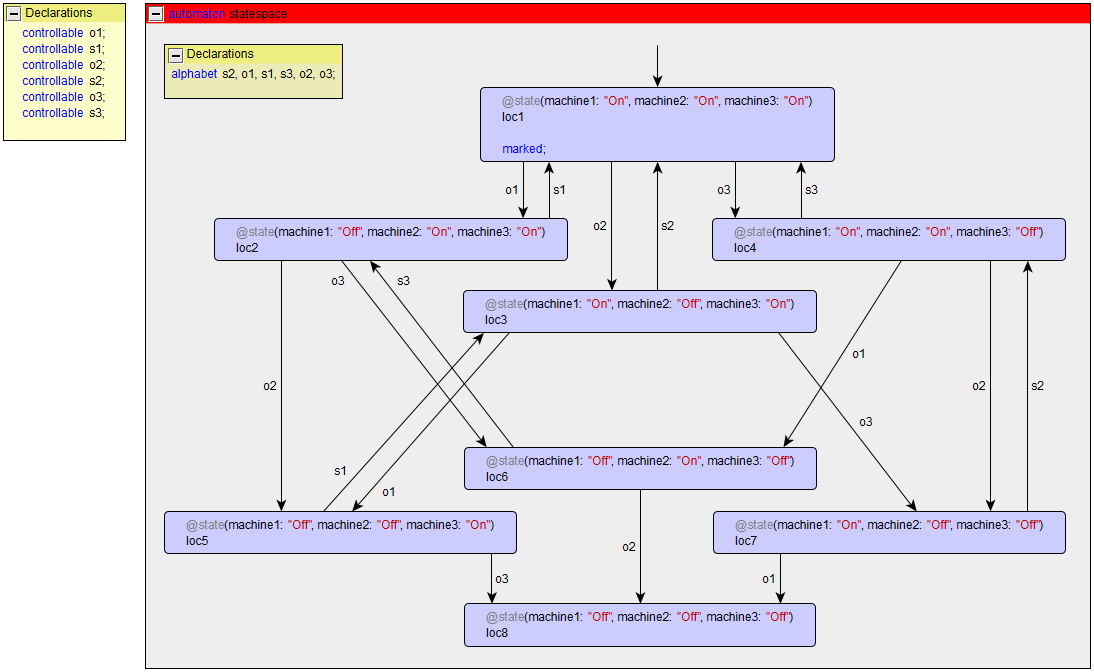
b. Is a supervisor needed? Explain your answer.
If all three machines are off at the same time, the system is in a deadlock. A supervisor should be synthesized to prevent this deadlock.
c. Manually synthesize a supervisor for this system, by following the steps of the synthesis algorithm. What restrictions does the synthesized supervisor impose?
The synthesized supervisor looks like this:
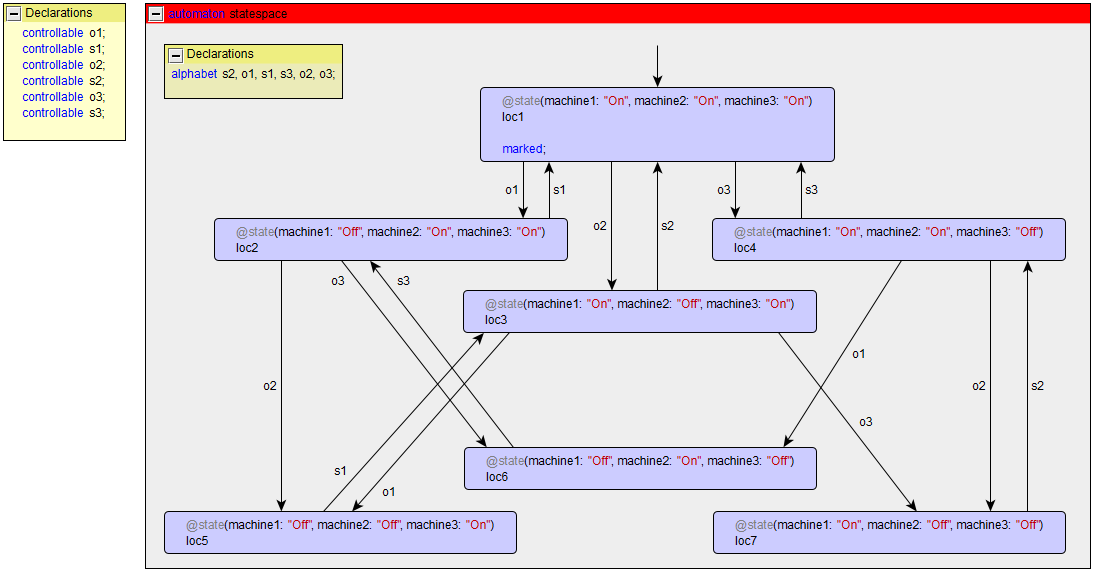
The state where all three machines are off, is removed. All the transitions leading to this state are disabled. For instance, when only machine 3 is on, the event to turn machine 3 off is disabled.
d. Remodel the system, making use of the fact that the three plant automata are very similar, while preserving the state space.
Hint: The three machine automata are the same except for the events they use on the edges. Use one plant automaton definition with event parameters and three instantiations.
The three instantiations have the same names as the original automata, to ensure the components' names are preserved.
controllable o1, s1;
controllable o2, s2;
controllable o3, s3;
plant def Machine(controllable start, off, allow):
location On:
initial;
marked;
edge allow;
edge off goto Off;
location Off:
edge start goto On;
end
machine1: Machine(s1, o1, s2);
machine2: Machine(s2, o2, s3);
machine3: Machine(s3, o3, s1);
Exercise 5
You are going to model cannibalistic rabbits. The rabbits have locked themselves in their rabbit hole and can't get any food. So, the rabbits start feeding on each other. Luckily, two rabbits can reproduce, leading to a new rabbit in the rabbit hole, ensuring food security in the long run. The rabbit hole can only house 4 rabbits. The initial population size is 3 rabbits. Furthermore, the rabbits can eat themselves out of desperation when no other rabbits are left.
Model the population size of the rabbits as a plant model, on paper. Also, derive a supervisor if necessary.
The population size can be modeled as a plant as follows:

Once there are less than two rabbits, the population will die out, resulting in deadlock. A supervisor should therefore be synthesized that prevents the rabbit from eating each other when the population size is two. Though, good luck explaining this to a rabbit. We opt to make all stable states marked. The synthesized supervisor is then as follows:
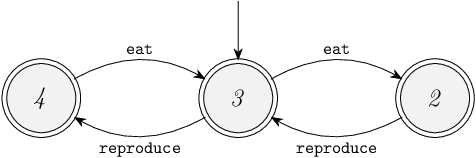
Exercise 6
Model the plant state space from the example on which the synthesis algorithm was explained earlier in this module, as a single CIF automaton. In the same CIF model, model the final three-state supervisor that was synthesized for it.
Then, check whether it makes a difference if the alphabet of the supervisor is the same as the plant or is b, d, e, f.
Hints:
- Define all events globally and define explicit alphabets for both automata.
- Ignore any warnings about certain events not being used on any edge.
- Compute the state spaces of both controlled systems and compare them, to see whether the different alphabets matter.
The plant state space, together with the supervisor with the full plant alphabet, can be modeled as follows in CIF:
controllable a, b, c, d, e;
uncontrollable f;
plant p:
alphabet a,b,c,d,e,f;
location l11:
edge c goto l21;
edge e goto l31;
location l21:
edge d goto l11;
edge b goto l22;
edge f goto l31;
location l22:
initial;
edge a goto l21;
edge b;
edge d goto l12;
edge f goto l32;
location l12:
edge a goto l11;
edge e goto l32;
location l31:
edge e;
location l32:
marked;
edge a goto l31;
edge e;
end
supervisor s:
alphabet a, b, c, d, e, f;
location l22:
initial;
edge b;
edge d goto l12;
edge f goto l32;
location l12:
edge e goto l32;
location l32:
marked;
edge e;
end
The variant where the supervisor has a smaller alphabet can be obtained by changing the explicit alphabet declaration of supervisor automaton s.
When the alphabet of the plant and supervisor are the same, the supervisor is a proper supervisor. It then disables all relevant events, resulting in the correct controlled system state space. When the supervisor alphabet is reduced, certain events are no longer restricted by the supervisor, and the controlled system contains undesired behavior.