Module 5.3: Continuous variables

Variable time tracks the absolute time that has passed in a model, since the initial state. However, often it is more convenient to use relative time. Relative time is the time that has passed since a certain moment in time, for example the time that has passed since the last occurrence of a certain event. To measure relative time, CIF features continuous variables. Continuous variables can however also be used to represent other continuously changing values, such as temperature, water levels, positions of moving objects, and so on.

Just like variable time, continuous variables change automatically as time progresses. However, there are differences. Continuous variables can also be assigned a new value on edges, like discrete variables, allowing for instance to reset them to zero. In addition, continuous variables can be initialized to any value, like discrete variables. Furthermore, the rate of change of the value of a continuous variable per time unit (that is, its derivative measured in seconds) can be different for every continuous variable. If a continuous variable has a derivative of one, either positive or negative, it is also called a timer.

The following CIF model shows an example of a continuous variable (more specifically, a timer), to model a lamp that is turned off five seconds after it is turned on:

                        
                            automaton lamp:
                                event turn_on, turn_off;
                                cont t = 0 der 1;

                                location Off:
                                    initial;
                                    marked;
                                    edge turn_on do t := 0 goto On;

                                location On:
                                    edge turn_off when t >= 5 goto Off;
                            end
                        
                    

The automaton models a lamp that can be turned on and off. Continuous variable t is declared in the automaton. It has initial value 0 and its derivative is 1. It thus starts at value 0, and every second it grows by 1. It is thus 1 after one second, 2 after two seconds, 2.5 after 2.5 seconds, and so on. Whenever event turn_on occurs, t is reset to zero, and time thus starts to be measured again from zero. The lamp is turned off only after 5 seconds have passed. When the lamp is turned on again, t is reset again, and time starts to measure from zero. So, the lamp is always turned off after having been on for 5 seconds.

Using a continuous variable is much easier than using variable time in this case. There is no need to separately account for 5, 10, 15, and so on seconds of time that have passed. Since there are infinitely many such times, they can't be listed individually. It would be possible to store the current time in a discrete variable when the lamp is turned on, and compare the current time against that variable, to see if five seconds have passed:

                        
                            automaton lamp:
                                event turn_on, turn_off;
                                disc real start_time;

                                location Off:
                                    initial;
                                    marked;
                                    edge turn_on do start_time := time goto On;

                                location On:
                                    edge turn_off when time - start_time >= 5 goto Off;
                            end
                        
                    

However, using a continuous variable leads to a simpler model, that more directly expresses our intent. We measure the relative time from the moment that the lamp is turned on in t, and check whether 5 seconds have passed using guard t >= 5.

Just as integer discrete variables have initial value zero if its not explicitly specified, so do continuous variables. The declaration of t can thus also be written as follows:

                        
                            cont t der 1;
                        
                    

Continuous variables may be declared in automata. Just as with discrete variables, only the automaton that declares the variable can assign it a new value. However, continuous variables may also be declared outside automata. They can then still be given an initial value and derivative, but they cannot be reset on edges.

Specifying derivatives

So far, we've specified the derivative of the continuous variable with its declaration. However, there are alternatives. We'll explore these alternatives using an example of a mobile phone:

                        
                            automaton phone:
                                event charge;
                                cont t = 0 der 1;

                                location:
                                    initial;
                                    marked;
                                    edge charge when t >= 100 do t := 0;
                            end
                        
                    

We'll consider a time unit to be a minute here. The phone can then be used for 100 minutes, after which it needs to be charged. It can then again be used for 100 minutes, before it needs to be charged again. The continuous variable again has its derivative defined with its declaration.

The derivative may alternatively be specified separately from the declaration of the continuous variable, using an equation:

                        
                            automaton phone:
                                event charge;

                                cont t = 0;
                                equation t' = 1;

                                location:
                                    initial;
                                    marked;
                                    edge charge when t >= 100 do t := 0;
                            end
                        
                    

The continuous variable is still declared in the automata, and still given an initial value of 0. However, its derivative is now specified by an equation. The equation t' = 1 indicates that the derivative of t, denoted by t', is 1. An equation for a continuous variable must be specified in the same component as where the continuous variable is declared. So, if a continuous variable is declared in an automaton, the equation must be in the same automaton. If a continuous variable is declared in a group, the equation must be in the same group. And if the continuous variable is declared outside the automata and groups, then the equation must be specified there as well. Separating the specification of the derivative from the declaration of the continuous variable can be useful for larger models.

This model is still a somewhat simplified version of reality, since the phone can be charged instantaneously. We can use the same continuous variable to measure the time that the phone can be used (100 minutes) and that it has to charge (10 minutes):

                        
                            automaton phone:
                                event charge, use;

                                cont t = 0;
                                equation t' = 1;

                                location Using:
                                    initial;
                                    marked;
                                    edge charge when t >= 100 do t := 0 goto Charging;

                                location Charging:
                                    edge use    when t >= 10  do t := 0 goto Using;
                            end
                        
                    

The automaton is extended to two locations, to track whether the owner is using the phone, or it is charging. After 100 minutes of using the phone, it needs to be charged, as indicated by the charge event occurring and the automaton going to the Charging location. After 10 minutes of charging, the phone can be used again, as indicated by the use event occurring and the automaton going to the Using location.

In reality, phones typically track the battery percentage, rather than measuring the time to the next charge. Let's assume the battery percentage drops by 1.5% per minute when the phone is being used, and it increases by 7% per minute when the phone is being charged. We can model the battery percentage using a continuous variable, and by specifying its derivative per location:

                        
                            automaton phone:
                                event charge, use;
                                cont battery_percentage = 100;

                                location Using:
                                    initial;
                                    marked;
                                    equation battery_percentage' = -1.5;
                                    edge charge when battery_percentage <   10 goto Charging;

                                location Charging:
                                    equation battery_percentage' = 7;
                                    edge use    when battery_percentage >= 100 goto Using;
                            end
                        
                    

The phone is initially fully charged, as indicated by its initial value of 100 percent. While the phone is being used, every minute the battery percentage drops by 1.5 percent, as specified by the equation in location Using. Once the phone's battery percentage drops under 10 percent, the phone is charged. Charging increases the battery percentage by 7 percent every minute. Once it is fully charged, it can be used again. By using an equation per location, we can make the battery percentage increase in one location and decrease in the other. We can also make it increase or decrease at different rates.

The derivative of a continuous variable may only be specified using equations per location, if the continuous variable itself is specified in that same automaton. An equation must then be present in every location. An equation may also specify that the derivative is zero, meaning that the continuous variable does not change its value while being in that location.

There are thus three ways to specify the derivative of a continuous variable: with its declaration, using a single equation, or using an equation per location of the automaton.

The model that specifies an equation per location can also be rewritten to use a single equation, by making use of an if expression:

                        
                            automaton phone:
                                event charge, use;
                                cont battery_percentage = 100;
                                equation battery_percentage' = if Using: -1.5 else 7 end;

                                location Using:
                                    initial;
                                    marked;
                                    edge charge when battery_percentage <   10 goto Charging;

                                location Charging:
                                    edge use    when battery_percentage >= 100 goto Using;
                            end
                        
                    

This brings the different values of the derivative closer together, which is especially useful if there are many locations and the values becomes a bit scattered throughout the model. The equation can also be written using a switch expression, which is slightly nicer in this case, as it makes the locations more explicit:

                        
                            automaton phone:
                                event charge, use;
                                cont battery_percentage = 100;
                                equation battery_percentage' = switch phone:
                                                                   case Using:    -1.5
                                                                   case Charging:  7
                                                               end;

                                location Using:
                                    initial;
                                    marked;
                                    edge charge when battery_percentage <   10 goto Charging;

                                location Charging:
                                    edge use    when battery_percentage >= 100 goto Using;
                            end
                        
                    

The switch expression has different cases, and for each case it can give a different value. In this case, it switches over automaton phone, meaning it switches over the locations of that automaton. Per location, it then indicates the derivative value. Since this switch expression is used inside the phone automaton, we can also use keyword self instead of the automaton name:

                        
                            equation battery_percentage' = switch self:
                                                               case Using:    -1.5
                                                               case Charging:  7
                                                           end;
                        
                    

Using self makes it easier to later change the automaton name.

This model is still somewhat unrealistic, as there is no way to use the phone for only half an hour, or charge it for only a minute. We'll revisit this in the next sub-module.

CIF simulator's plot visualizer

When simulating models with timed behavior, the CIF simulator's state visualizer will also show the value of variable time and each continuous variable. However, it only shows the values for the current state (that is, only the value that it has at the current time). When dealing with timed behavior, it can be very useful to see the values of the variables as they change over time. The CIF simulator features a plot visualizer for that. It displays a graph of the values of the variables over time. It can be enabled in a similar way as the state visualizer.

If we simulate the lamp that is only on for 5 seconds (see top of this page) for 40 time units, the plot visualizer shows:

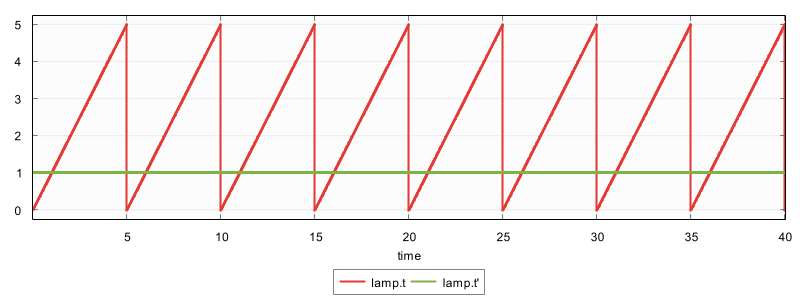
We see the value of continuous variable lamp.t over time, but also that of its derivative lamp.t'.

Quiz