Module 3.3: Supervisory controller synthesis

Now that you know about the controllability, non-blockingness and maximal-permissiveness guarantees of supervisory controller synthesis, it is time to look at the synthesis algorithm itself. The synthesis algorithm constructs a proper supervisor, in a systematic way. That is, given a plant model model, the algorithm computes a controllable, non-blocking and maximally-permissive supervisor. First, we look at a simple example. And then we discuss the general steps that are involved in the synthesis algorithm.

Do keep in mind that in this module, user-provided requirements and the associated safety guarantee are not yet considered. Since they are covered later in Module 4, the algorithm as we discuss it here is not yet the full algorithm.

Example

Consider the automata shown below. They are adapted versions of the automata from the quiz of the module on synchronizing automata. The initial and marked locations have changed, and event f has become an uncontrollable event. Other than that, they are the same.

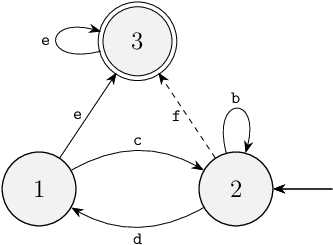
The synthesis algorithm is easier to explain when applied to a single automaton, rather than to multiple ones. Therefore, we first compute the state space automaton of the two automata above, which is shown below. The actual synthesis algorithm in CIF does not first construct the full state space before computing the supervisor. Instead, it computes the supervisor directly from the multiple automata, in a more efficient manner. Conceptually though, the task of synthesizing a supervisor is the same.

Through synthesis, a supervisor is derived from the plant model. You may have already noticed that state (3, 1) is blocking state, since it is not a marked state, and no marked state can be reached from it. The supervisor should prevent the system from getting into this state, to avoid blocking behavior. The state is a bad state and is thus removed. And as a consequence of removing it, all its outgoing transitions are also no longer possible. The self-loop transition on state (3, 1) can thus never be taken anymore:

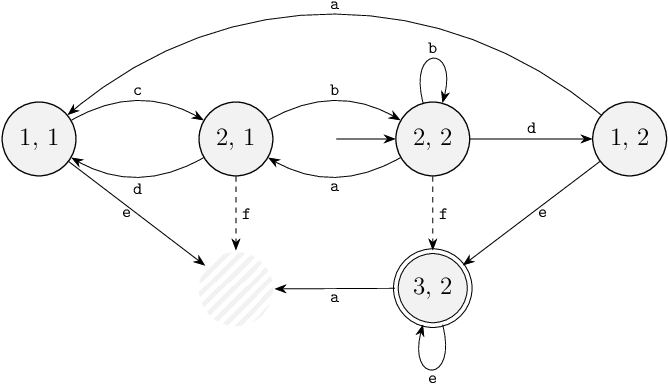
To make sure the removed state can never be reached, the supervisor has to disable all transitions leading to that state. In this case, that concerns three transitions: the transition from state (1, 1) for event e, the transition from state (2, 1) for event f, and the transition from state (3, 2) for event a. Out of these three transitions, two transitions are for controllable events. These two transitions can be directly disabled by the supervisor.

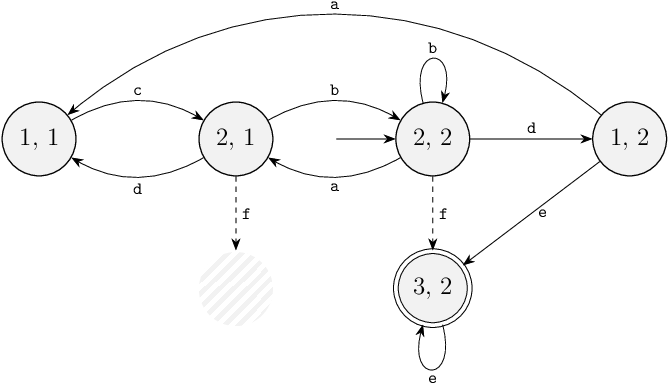
The third transitions is for an uncontrollable event. A supervisor may never disable uncontrollable events, as that would violate the controllability guarantee. Therefore, the supervisor must thus ensure that state (2, 1) is never reached, since if it would be reached, then through an uncontrollable event that the supervisor can't prevent, the system could end up in a blocking state, namely removed state (3, 1). State (2, 1) is thus a bad state, and is removed. Its outgoing transitions are then also no longer possible:

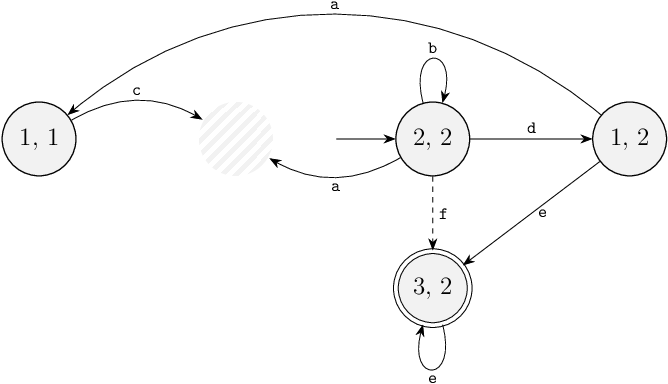
Then there are the two transitions to removed state (2, 1) to consider. The transitions from state (1, 1) for event c and the transitions from state (2, 2) for event a, both involve controllable events. The supervisor can thus disable them directly:

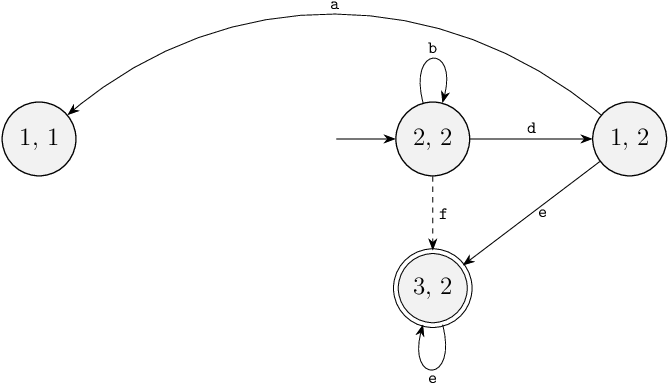
We have now completed one iteration of removing blocking states, while ensuring controllability is preserved. However, state (1, 1) has now become a blocking state. It is thus a bad state, and is removed. It has no incoming transitions for uncontrollable events. It has one incoming transition, the transition for from state (1, 2) for controllable event a. Event a is thus disabled in state (1, 2):

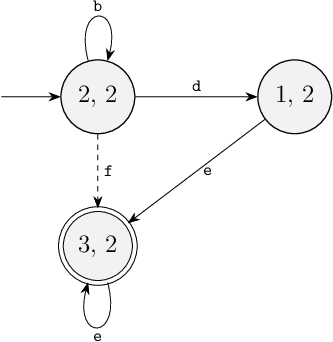
We have now completed two iterations of removing blocking states, while ensuring controllability is preserved. This automaton is a controllable, non-blocking and maximally-permissive supervisor for this example.

Note that its alphabet is the same as the original automaton, and thus includes events a, b, c, d, e and f. That is, it has an alphabet containing events that are not on any of the edges of the automaton, namely events a and c. In a CIF model of this automaton, this alphabet would thus need to be explicitly declared, to ensure the supervisor properly disables these events. Without the explicit alphabet, a plant automaton with an edge for event a could still take that edge, since the supervisor would not synchronize on the event and would thus not disable it. Hence, such a supervisor automaton always has the same alphabet as the plant.

The synthesis algorithm

For the example above, we started with the state space of the plant. We then systematically removed non-blocking states and ensured controllability is preserved, while only removing states and transitions where it was necessary.

In general, the synthesis algorithm takes the uncontrolled plant as the initial supervisor. It then performs the following steps to turn it into a proper supervisor, repeating the steps if any of them led to removing any states or disabling any transitions:

1. Determine all blocking states. Mark them as bad states and remove them.
2. Determine all non-controllable states, the states from which an uncontrollable-event transition is possible to a bad state. Mark them as bad states and remove them.
3. Optionally, determine all unreachable states. Mark them as bad states and remove them.
4. Disable all transitions for controllable events in states where they lead to a bad state.

Quiz

[ { type: 'single-choice', question: "What would be a controllable, non-blocking and maximally-permissive supervisor for the example above, if plant state (3, 1) would be a marked state instead of state (3, 2)?", answers: [ "The supervisor that was the result of the first iteration as discussed above.", "The supervisor that was synthesized for the example still suffices.", "Since the only blocking location is now marked, the plant itself can in this case serve as a controllable, non-blocking and maximally-permissive supervisor." ], correctAnswer: '3' }, { type: 'single-choice', question: "What would be a controllable, non-blocking and maximally-permissive supervisor for the example above, if plant state (1, 2) would be the initial state instead of state (2, 2)?", answers: [ "The supervisor that was the result of the first iteration as discussed above.", "The supervisor that was synthesized for the example still suffices.", "The supervisor that was synthesized for the example is adapted by removing unreachable state (2, 2), such that only states (1, 2) and (3, 2) remain.", "Since the only blocking location is now marked, the plant itself can in this case serve as a controllable, non-blocking and maximally-permissive supervisor." ], correctAnswer: '3' }, { type: 'single-choice', question: "What are the four steps of the supervisory controller synthesis algorithm?", answers: [ "1: Remove all blocking states. 2: Remove all non-controllable states. 3: Remove all unreachable states. 4: Remove all controllable-event transitions to removed states.", "1: Remove all non-controllable states. 2: Remove all blocking states. 3: Remove all unreachable states. 4: Remove all controllable-event transitions to removed states.", "1: Remove all non-controllable states. 2: Remove all blocking states. 3: Remove all controllable-event transitions to bad states. 4: Remove all unreachable states.", "1: Remove all blocking states. 2: Remove all controllable-event transitions to bad states. 3: Remove all unreachable states. 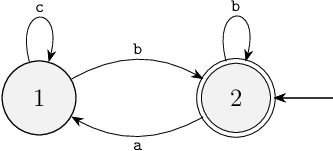4: Remove all uncontrollable-event transitions to bad states.", ], correctAnswer: '1' }, { type: 'multiple-choice', question: ` Consider the following two alternative supervisors for the example above. Are these also proper controllable, non-blocking and maximally-permissive supervisors, like the one we synthesized? Hint: Consider the uncontrolled system state space versus the controlled system state space, for the plant combined with each of these alternative supervisors. `, answers: [ "The left automaton is a proper alternative supervisor.", "The right automaton is a proper alternative supervisor." ], correctAnswer: '2' }, { type: 'single-choice', question: ` What happens if synthesis is applied to the following plant model? `, answers: [ "The plant is the same as the supervisor.", "Synthesis removes all states, except for the initial state.", "All states are bad, and thus no supervisor can be computed.", ], correctAnswer: '2' }, { type: 'single-choice', question: ` What happens if synthesis is applied to the following plant model? `, answers: [ "The plant is the same as the supervisor.", "Synthesis removes all states, except for the initial state.", "All states are bad, and thus no supervisor can be computed.", ], correctAnswer: '3' } ]