Problems with root finding
With numeric root finding, there is the risk of missing guard changes, which means there is the risk of missing event transitions.
The problem
To illustrate the problem, consider the following CIF specification:
automaton p:
cont x = 0.0;
equation x' = 1.0;
location:
initial;
edge when x >= 2.33 and x <= 2.34 do x := 0.0;
endThis specification, when simulated using the CIF simulator, using default settings, results in:
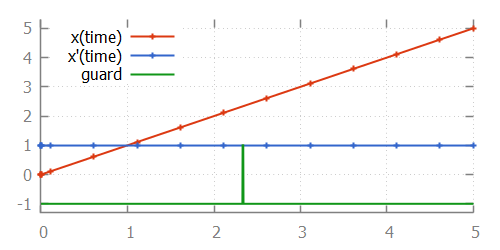
From the image, where the values calculated by the integrator are indicated using small plus signs (+), we can see that for times 2.1111 and 2.6111, the integrator calculated points. Since the function is linear between those two time points, no additional intermediate time points were investigated. Since the guard becomes true after time point 2.1111 (at time point 2.33) and also becomes false again before time point 2.61111 (at time point 2.34), the integrator misses the guard change. That is, for every time point that the guard is evaluated, it is false, and the change in guard value is thus not detected. We miss the guard, and thus the event that resets variable x to 0.0.
Solution 1: maximum check interval
The first solution is to use the ODE solver root finder maximum check interval option (ODE solver: ODE root finder category). This option can be used to set the maximum time interval between two consecutive checks of the sign of the guard. By default, this is 0.5 time units. If we set this value to 0.001, then we ensure that at least once every 0.001 time units, the guard sign is checked. This means that between time points 2.1111 and 2.61111, the guard will be checked approximately 500 times. This also means that between time points 2.33 and 2.34, the guard will be checked approximately 10 times. Therefore, this ensures that we check a time point just before time 2.33, and one just after it, which means we can’t miss the guard change.
In the above example, x' is 1.0. If however x' would be 2.0, then the time interval where the guard is enabled reduces from 0.01 time units to 0.005 time units. Using a maximum check interval of 0.001 would then still suffice, as the guard would be checked approximately 5 times in that time interval. If however x' is 100, then the time interval would become 0.0001, which is smaller than the maximum check interval of 0.001. That is, the derivatives of the values occurring in guards influence the value that should be chosen for the maximum delay interval.
In general, to choose an appropriate value for the maximum check interval, not only the ranges of values of the variables where the guard is enabled should be taken into account, but the steepness of their derivatives as well. That is, the value of the maximum check interval should be based on the time interval where the guard is enabled. Choosing half the duration of the smallest of such time intervals, for all guards, is generally a good choice.
Note that choosing a smaller interval results in more guard change checks, and thus negatively impacts the performance of the simulation. Therefore, choosing a maximum check interval that is unnecessarily small also unnecessarily reduces performance of the simulation.
Solution 2: splitting the guard
We can reformulate the original CIF specification, by splitting the guard:
automaton p:
cont x = 0.0;
equation x' = 1.0;
location:
initial;
edge when x >= 2.33, x <= 2.34 do x := 0.0;
endThis specification, when simulated using the CIF simulator, using default settings, results in:
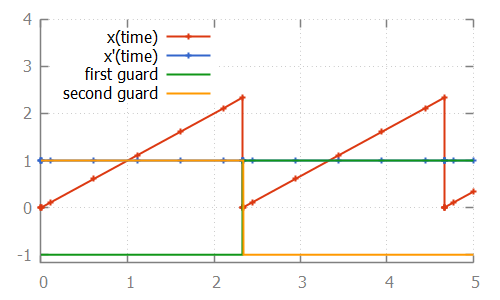
The difference with the original specification is the guard of the edge. In the original specification, the and binary operator is used, making it a single guard. In the new specification, a comma (,) is used, which constructs two separate guards. Both guards can be individually checked by the root finding algorithm. As shown in the image, each of the guards changes value only once.
The comma between guards means that both guards have to hold, in order for the edge to be enabled. This is similar, but not identical, to the and binary operator. For the and binary operator, the left hand side must be evaluated before the right hand side, and the right hand side may only be evaluated if the left hand side evaluates to true. This is called short-circuit evaluation. For guards separated by commas, no such relation may be assumed. That is, even if the first guard evaluates to false, can the second guard still be evaluated by the root finding algorithm, for guard changes. It can even be the case that the second guard is evaluated before the first guard. These differences not only influence root finding, but are also of particular interest when the right hand side can result in a runtime evaluation failure. For instance, the following specification:
automaton p:
cont x der 1.0;
location:
initial;
edge when x > 0, 1 / x < 0.5 do x := 0.0;
endresults in a runtime error. The second guard (1 / x < 0.5) is evaluated even if the first guard (x > 0) does not hold. Initially, the first guard does not hold, and the second guard results in division by zero. Changing the comma between the guards to an and operator, makes it possible to simulate this specification.
Debug information
Debug information about what the ODE solver calculates, and for what time points, can be enabled using the Debug output option. This may be useful in figuring out why the guard was missed, and what settings need to be changed. See the Debug console output page for more information.