Global read, local write
Discrete variables can only be declared in automata, and may only be assigned (given a value, written) by that automaton. They may however be read globally. Consider the following CIF specification:
automaton customer:
location:
initial;
edge queue1.enter when queue1.count <= queue2.count;
edge queue2.enter when queue2.count <= queue1.count;
end
automaton queue1:
event enter, leave;
disc int count = 0;
location:
initial;
edge enter when count < 2 do count := count + 1;
edge leave when count > 0 do count := count - 1;
end
automaton queue2:
event enter, leave;
disc int count = 0;
location:
initial;
edge enter when count < 2 do count := count + 1;
edge leave when count > 0 do count := count - 1;
endThis specification models a supermarket, and features a customer and two queues. Customers arrive and enter either of the queues. Eventually customers leave the queue.
Both queues (automata queue1 and queue2) are identical, except for their names. They maintain the count, which represents the number of customers in the queue. A queues is full if it contains two customers. Customers can thus only enter a queue if less than two customers are present. Similarly, it is only possible for a customer to leave a queue if there is a customer in the queue.
Customers decide to which queue they go, based on the number of customers already present in those queues. A customer only enters the first queue if that queue has less than or the same number of customers as the second queue. Similarly, a customer only enters the second queue if that queue has less than or the same number of customers as the first queue. If the queues have the same number of customers, the customer can choose either queue.
The enter event declared in the first queue (queue1) is used by both the customer automaton and the queue1 automaton. The event is thus only possible (enabled) if both automata can participate. Both automata restrict the occurrence of the event using a guard. The event is thus only possible if both guards hold. That is, a custom never enters the first queue if it is full, but it also never enters that queue if it has more customers than the second queue.
The state space of this specification is as follows:
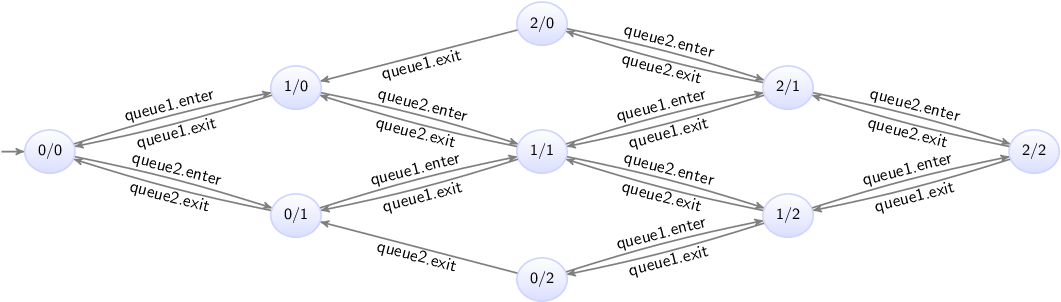
The states are labeled with the counts of the first and second queues.
The customer automaton uses the values of the variables of the queue automata, and thus reads variables of other automata. This is allowed, due to the global read concept of CIF. This concept allows for short guards, that directly and intuitively represent the condition under which an event may take place.
The global read concept should only be used when it is intuitive. In the supermarket example, the customer can physically see how many customers are in the queues. It is therefore intuitive to directly refer to the count variables of the queue automata. If however the customer would not be able to physically observer the queues, then the customer would not be able to directly base its decision of which queue to join, on that information. In that latter case, it may not be a good idea to model the guard in such way.
The local write concept means that discrete variables can only be written by the automata in which they are declared. It is not allowed for the customer and queue2 automata to write (change the value of) the count variable of the queue1 automaton. Only the queue1 automaton may write that variable. The local write concept prevents that multiple automata write to the same variable, as part of a synchronizing event, potentially causing conflicting values to be assigned to that variable. This leads to several benefits, most notably simpler semantics.