Continuous variables and equations
Consider the following CIF specification:
automaton person:
event turn;
cont t = 0 der 1;
location:
initial;
edge turn when t > 10 do t := 0.0;
endThis specification models a person walking back and forth. Every time that the person has walked 10 time units, (s)he will turn around, walking in the other direction.
In the example above, the derivative of the continuous variable is defined with the declaration, as was already explained in the lesson that introduced continuous variables. However, it also possible to specify the derivative separately, using an equation:
automaton person:
event turn;
cont t = 0; // Declaration specifies only the initial value.
equation t' = 1; // Derivative specified using separate equation.
location:
initial;
edge turn when t > 10 do t := 0.0;
endThis allows for separation of variable declarations and equations. Both variants have the same continuous variable with the same derivative. An equation of a derivative of a continuous variable must be placed in the same component as where the continuous variable is declared. In the example above, the equation for t' must be placed in automaton person, as that is where t is declared.
We could extend this specification to keep track of the direction that the person is moving:
automaton person:
event turn;
cont t = 0 der 1;
location away:
initial;
edge turn when t > 10 do t := 0.0 goto back;
location back:
edge turn when t > 10 do t := 0.0 goto away;
endFor continuous variables declared in automata, it is also possible to specify the derivative using an equation per location of the automaton. This allows us to keep track of the exact position of the person:
automaton person:
event turn;
cont pos = 0;
location away:
initial;
equation pos' = 1;
edge turn when pos > 10 goto back;
location back:
equation pos' = -2;
edge turn when pos < 0 goto away;
endHere, the continuous variable t has been renamed to pos, to make it more clear that it indicates the position of the person. As long as the person is moving away, the derivative of pos is 1, and the person moves away, one place every time unit. When the person reaches position 10, the position is not reset to zero. Instead, only the location is changed to the back location. In that location, the derivative of pos is -2. This means that every time unit, the position decreases by 2. That is, the person back to the original position, but at twice the speed. The values of variables time, pos, and pos' as time progresses are:
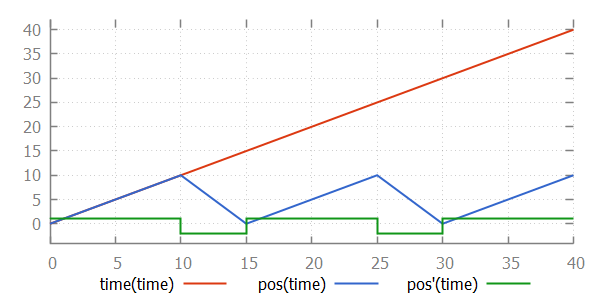
As with algebraic variables, every continuous variable must have a unique derivative in every situation. Continuous variables must thus have a derivative with their declaration, a single equation in the same component, or an equation in every location of the automaton. For every continuous variable, one of the three variants must be chosen. It is allowed to choose a different variant for different continuous variables, but it is not allowed to use multiple variants for the same continuous variable.